Peatüki algus: Lineaarsete algebraliste võrrandisüsteemide lahendamise
Järgmine: Positiivselt määratud süs teemid

Vaatleme järgnevalt ruutmaatriksi LU-lahutuse erijuhte.

Lause 6.1.1. Kui maatriksi kõik peamiinorid on nullist erinevad, siis eksisteerivad sellised ühikpeadiagonaaliga alumised kolmnurkmaatriksid L ja M ning diagonaalmaatriks et
 
kusjuures lahutus (1) on ühene.

Tõestus. Kuna maatriksi kõik peamiinorid on nullist erinevad, siis lause 1.2.2 põhjal leidub maatriksil A ühene LU-lahutus
 
Olgu kus d_i=u_ii (i =1: n). Maatriksi A regulaarsusest järeldub, et maatriks D on regulaarne. Seega, ja M^T=D^-1U on ülemine ühikdiagonaaliga kolmnurkmaatriks. Järelikult,

Lahutuse (1) ühesus järeldub lahutuse (2) ühesusest.

Definitsioon 6.1.1. Lahutust (1) nimetatakse regulaarse maatriksi LDM^T-lahutuseks.

Näide 6.1.1.^* Leiame maatriksi

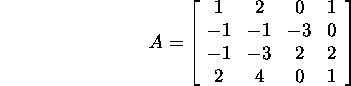
LDM^T-lahutuse. Nendime, et kui maatriksi A peamiinorid on nullist erinevad, siis maatriksi A viimisel Gaussi teisenduse abil kolmnurkkujule, leiame samaaegselt nii maatriksi L kui ka maatriksi U. Nimelt, alumise kolmnurkmaatriksi L element l_ij võrdub teguriga, millega tuleb j-ndat rida korrutada mahalahutamisel i-ndast reast i-ndas reas oleva elemendi nullistamisel. Leiame, et



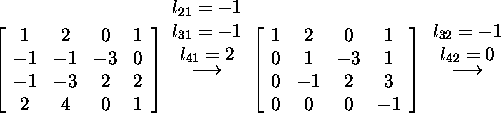
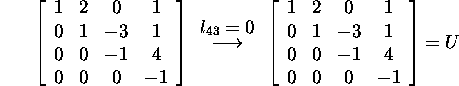
ja

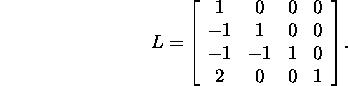
Teostame kontrolli:

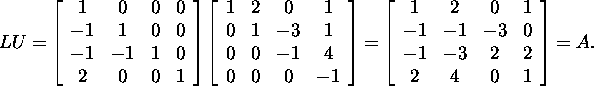
Lause 6.1.2. Kui regulaarne maatriks on sümmeetriline ja selle maatriksi LDM^T-lahutus on kujul (1), siis L=M, st
 

Tõestus. Lahutusest (1) järeldub, et

Korrutades viimase seose mõlemat poolt vasakult maatriksiga M^-1, saame seose
 
Maatriks M^-1AM^-T on sümmetriline, sest

Maatriks M^-1AM^-T on alumine kolmnurkmaatriks, sest nii M^-1 kui ka AM^-T=LD on alumised kolmnurkmaatriksid. Seose (4) põhjal on sümmeetriline ja alumine ka kolmnurkmaatriks M^-1LD. Seega, maatriks M^-1LD on diagonaalne. Kuna maatriks D on regulaarne, siis on diagonaalne ka maatriks M^-1L. Lisaks on maatriks M^-1L ühikdiagonaaliga alumine kolmnurkmaatriks. Järelikult, M^-1L=I ehk

Ülesanne 6.1.1.^* Leidke maatriksi

LU-lahutus, LDM^T-lahutus ja LDL^T-lahutus.

s