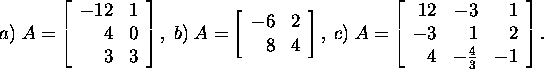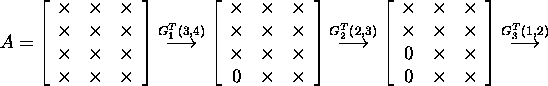
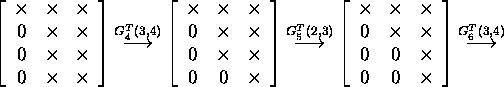
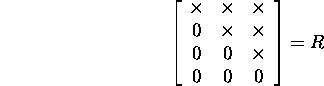
Ortogonaalmaatriks avaldub kujul:
Peatüki
algus: QR-lahutus
Eelmine: Householderi
QR-lahutus
Järgmine: QR-lahutuse
põhiteoreem
Vaatleme järgnevas Givensi pöörete kasutamist maatriksi QR-lahutuse saamiseks.
Näide 2.4.1. Vaatleme
![]() korral Givensi QR-lahutuse skeemi:
korral Givensi QR-lahutuse skeemi:
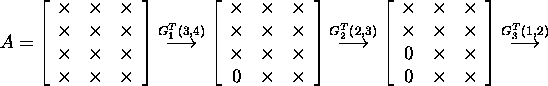
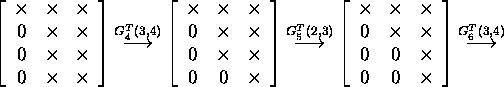
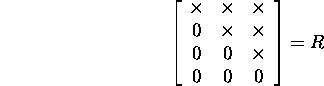
Ortogonaalmaatriks avaldub kujul:
![]()
Näide 2.4.2.* Leiame maatriksi
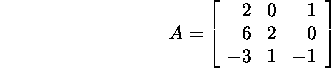
Givensi QR-lahutuse.
Muudame nulliks maatriksi A elemendi A(3,1). Selleks moodustame
Givensi maatriksi G1(2,3).
Leiame suuruste c ja s väärtused:
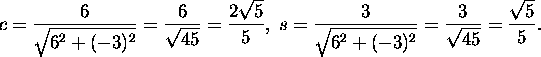
Seega saame, et
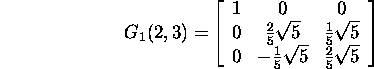
ja
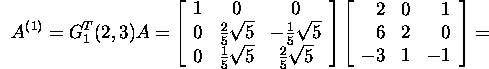
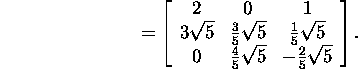
Muutmaks nulliks maatriksi A(1) elementi A(1)(2,1)
moodustame Givensi maatriksi G2(1,2).
Leiame suuruste c ja s väärtused:
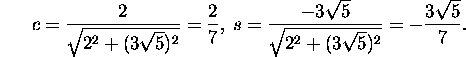
Seega
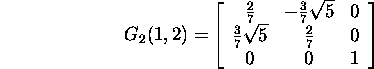
ja
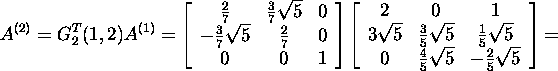
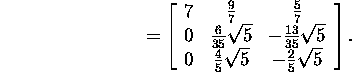
Muutmaks nulliks maatriksi A(2) elementi A(2)(3,2)
moodustame Givensi maatriksi G3(2,3).
Leiame suuruste c ja s väärtused:
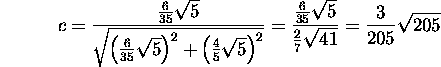
ja
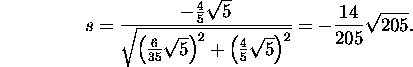
Seega
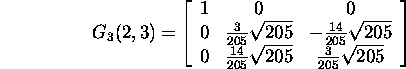
ja
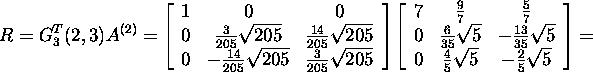
:
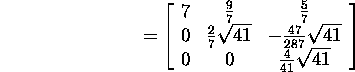
ning
![]()
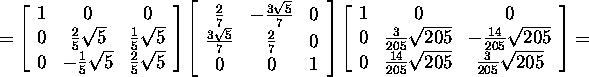
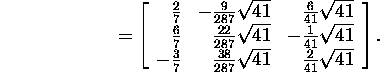
Kontrollime:
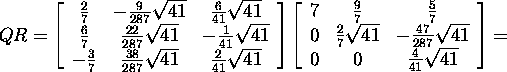
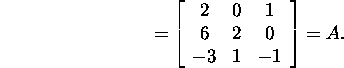
Ülesanne 2.4.1. Leidke näites 2.3.2 antud maatriksi A Givensi QR-lahutus.
Ülesanne 2.4.2.* Leidke
maatriksi A Givensi QR-lahutus,
kui