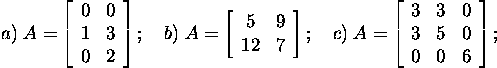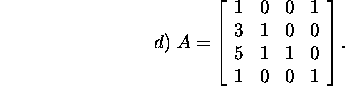Peatüki
algus: QR-lahutus
Eelmine: Givensi
pöörete meetod.
Järgmine: Givensi
QR-lahutus
Kasutame Householderi
teisendust maatriksi ![]() korral QR-lahutuse
saamiseks.
korral QR-lahutuse
saamiseks.
Näide 2.3.1. Olgu ![]() ning olgu Householderi maatriksid
H1 ja H2 juba nii leitud, et
ning olgu Householderi maatriksid
H1 ja H2 juba nii leitud, et
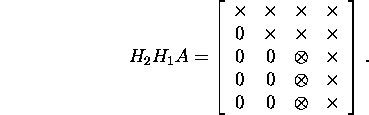
Vaatleme märgitud vektorit ![]() ja koostame sellise Householderi maatriksi
ja koostame sellise Householderi maatriksi
![]() et
et
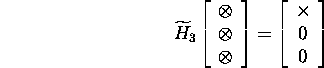
ning kui valida ![]() siis
siis
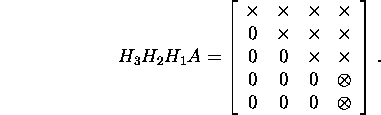
Järgmisena vaatleme märgitud vektorit ![]() ja koostame sellise
ja koostame sellise ![]() ,
et
,
et
![]()
ning valides ![]() saame
saame
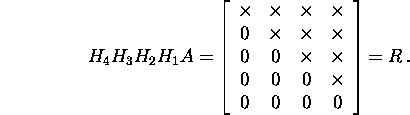
Kui valida Q=H1H2H3H4,
siis QR=H1H2H3H4H
4H3H2H1A=A.
Lause 2.3.1. Kui
![]() siis leiduvad sellised Householderi
maatriksid
siis leiduvad sellised Householderi
maatriksid ![]() et
et
![]()
ja
![]()
ning
![]()
kusjuures ![]() on ortogonaalmaatriks ja
on ortogonaalmaatriks ja ![]() on ülemine kolmnurkmaatriks.
on ülemine kolmnurkmaatriks.
Näide 2.3.2. Leida
maatriksi
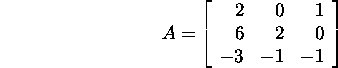
Householderi QR-lahutus. Näites
2.1.1 on leitud maatriksi A esimese veeruvektori ![]() teisendamiseks sobiv Householderi maatriks
teisendamiseks sobiv Householderi maatriks
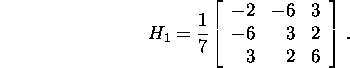
Leiame, et
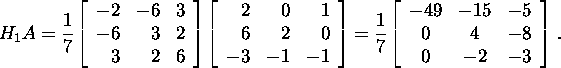
Maatriksi ![]() leidmiseks leiame vastava Householderi
vektori
leidmiseks leiame vastava Householderi
vektori
![]()
Seega
![]()
ja
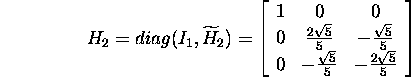
ning
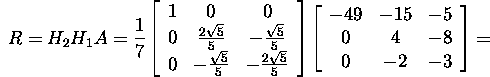
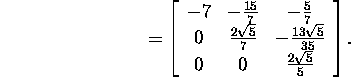
Leiame samuti ortogonaalmaatriksi
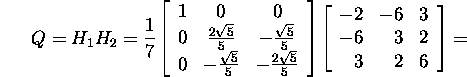
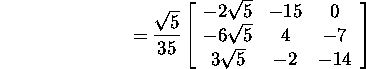
ning teostame kontrolli
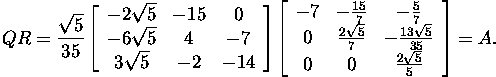
Näide 2.3.3*.
Leiame maatriksi

Householderi QR-lahutuse.
Teisendatav vektor on ![]() kusjuures
kusjuures ![]() Moodustame vektori
Moodustame vektori
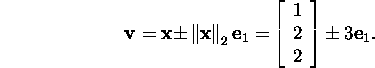
Valime vektori ![]() miinuskordse ning arvestame, et maatriks H sõltub vaid vektori
miinuskordse ning arvestame, et maatriks H sõltub vaid vektori
![]() sihist:
sihist:
![]()
Leiame Householderi maatriksi
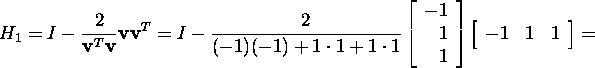
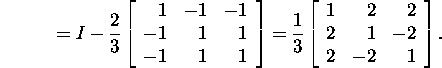
Veendume, et maatriks H1 nullistab maatriksi A
esimese veeru elemendid alates teisest reast. Tõesti,
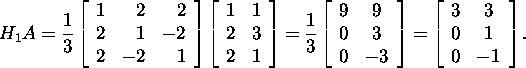
Edasi teisendame vektorit ![]() kusjuures
kusjuures ![]() Leiame sellele vektorile
Leiame sellele vektorile ![]() vastava Householderi vektori
vastava Householderi vektori
![]()
Valime vektori ![]() miinuskordse:
miinuskordse:
![]()
Saame sellele vektorile vastava Householderi
maatriksi
![]()
![]()
![]()
ja leiame, et
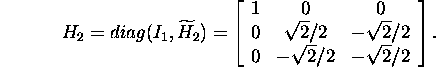
Seega
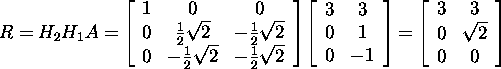
ja
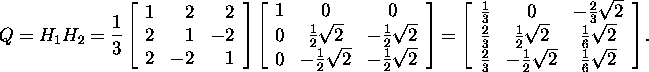
Teostame kontrolli:
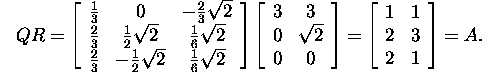
Ülesanne 2.3.1.* Leidke
maatriksi A Householderi QR-lahutus,
kui