Peatüki algus: QR-lahutus
Eelmine: QR-lahutus
Järgmine: Givensi pöörete meetod.

Definitsioon 2.1.1. Kui ja siis maatriksit
 
nimetatakse Householderi maatriksiks ehk Householderi teisenduse maatriksiks ning vektorit Householderi vektoriks.

Lause 2.1.1. Householderi maatriks H on sümmeetriline ja ortogonaalne maatriks. Householderi teisendus peegeldab iga hüpertasandi suhtes.

Tõestus. Tõesti,

ja

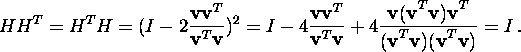
Lause väite kolmanda osa tõestamiseks valime hüpertasandil ristbaasi Järelikult, (i = 1 : ) ja = 1 :. Kui

siis







st vektoritel ja on hüpertasandil sama ristprojektsioon

kuid projektsioonid vektorile on vastassuunalised. Seega on vektori peegeldus hüpertasandi suhtes. Oluline on märkida, et Householderi maatriks H sõltub vaid Householderi vektori sihist ja ei sõltu vektori suunast ega pikkusest.

Lause 2.1.2. Kui ja siis vektor , kus H on seosega (1) määratud Householderi maatriks, on vektori sihiline vektor, st et Householderi teisendus H rakendatuna vektorile nullistab vektori koordinaadid alates teisest koordinaadist.

Tõestus. Üritame fikseeritud nullist erineva vektori korral määrata Householderi vektorit nii, et Kuna

ja siis Valides saame, et



ja



Valime selliselt, et viimases esituses vektori kordaja on null, st





Sellise valiku korral ja

Näide 2.1.1 Olgu Leiame sellise Householderi vektori ja sellele vastav Householderi teisenduse, mis nullistab vektori kaks viimast koordinaati. Lause 2.1.1 põhjal arvutame Valime vektori plusskordse ja saame 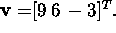Leiame Housholderi maatriksi H, arvestades, et H sõltub vaid vektori sihist,



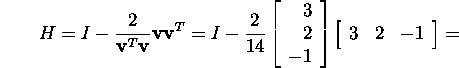
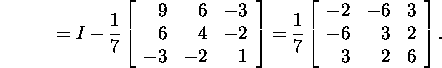
Kontrollime,

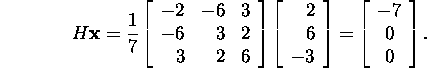
Ülesanne 2.1.1^* Leidke selline Householderi maatriks H, et , kus

Olgu (= 1:) Householderi maatriksid. Vaatleme nende maatriksite korrutist

kusjuures

ja iga on kujul

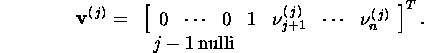
Maatriksit Q võib esitada kujul
 
kus W ja Y on maatriksid. Vastuse küsimusele, kuidas leida esitust (2), annab järgmine lause.

Lause 2.1.3. Olgu maatriks ortogonaalne, kusjuures Kui kus ja siis

kus ja ning seega, W₊,

Tõestus. Kuna



ja

siis ja lause väide on tõene.

Peatüki algus: QR-lahutus
Eelmine: QR-lahutus
Järgmine: Givensi pöö rete meetod.