Peatüki algus: Maatriksid
Eelmine: Maatriksi normid ja konditsiooniarvud
Järgmine: Maatriksargumendiga funktsioonid

Lause 2.8.1 (Cayley-Hamiltoni teoreem). Kui ja

siis p(A)=0, st maatriks A rahuldab oma karakteristlikku võrrandit.

Tõestus. Lause 2.6.7 põhjal leidub selline regulaarne et

kusjuures

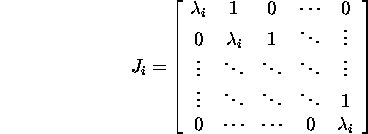
on ülemine bidiagonaalne -maatriks (Jordani blokk), mille peadiagonaalil on maatriksi A omaväärtus ( vähemalt m_i-kordne maatriksi A omaväärtus, sest sellele omaväärtusele võib vastata veel teisi Jordani blokke) ja Kuna siis ja )^m_i=0. Kui on maatriksi A karakteristlik polünoom ja selle polünoomi nullkohad, siis

ja

Näitame, et p(J)=0. Olgu maatriks J blokk-kujul

Saame, et















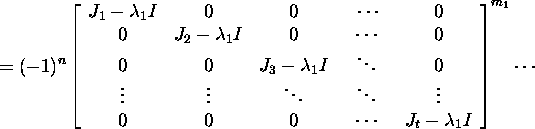
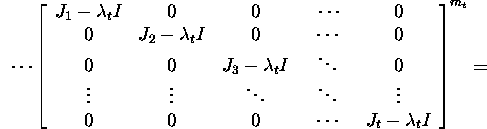
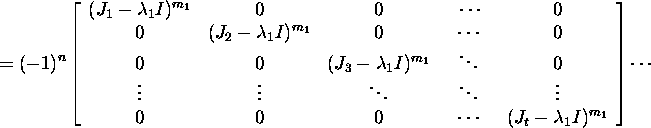
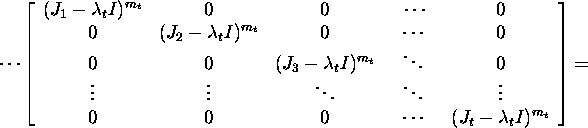
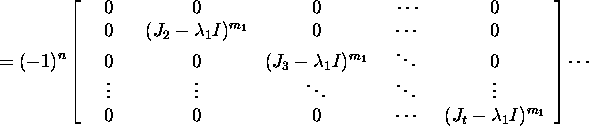
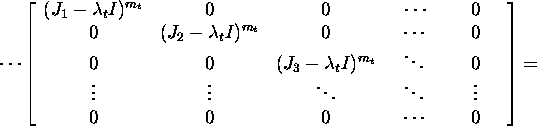
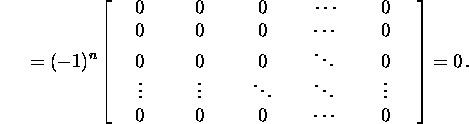
Seosest X^-1AX=J äreldub, et A=XJX^-1. Tõestuse viime lõpule ahelaga

Näide 2.8.1. Veenduda Cayley-Hamiltoni teoreemi väites maatriksi

korral. Koostame karakteristliku polünoomi

ja leiame

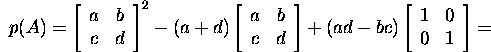
Ülesanne 2.8.1.^* Olgu

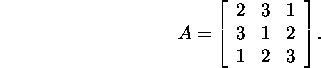
Arvutage A² ja kasutades Cayley-Hamiltoni teoreemi leidke maatriks

Definitsioon 2.8.1. Polünoomi nimetatakse maatriksit annulleerivaks polünoomiks, kui q(A)=0.

Maatriksi karakteristlik polünoom on (Cayley-Hamiltoni teoreemi põhjal) seda maatriksit annulleeriv polünoom.

Definitsioon 2.8.2. Maatriksi madalaimat järku annulleerivat polünoomi nimetatakse maatriksi A minimaalpolünoomiks.

Ülesanne 2.8.1. Veenduge, et maatriksi karakteristlik polünoom jagub jäägita maatriksi A minimaalpolünoomiga.

Lause 2.8.2. Olgu ja vastavalt maatriksi A karakteristlik polünoom ja minimaalpolünoom. Polünoomidest koosneva maatriksi mis on maatriksi -A) elementide algebraliste täiendite maatriks, elementide suurim ühistegur olgu . Siis

Tõestus. Vaadake Lankaster (1982, lk 123-124).

Näide 2.8.2. Leida maatriksi D=diag(a,a,b,b) karakteristlik polünoom ja minimaalpolünoom. Esmalt leiame, et





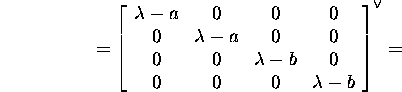
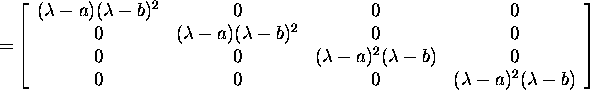
ja maatriksi elementide suurim ühistegur Lause 2.8.2 väitel Teostame kontrolli,



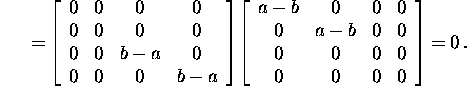
Tõesti, on maatriksit annulleeriv polünoom. On lihtne veenduda, et ükski esimest järku polünoom ei saa annulleerida maatriksit A. Seega on maatriksi A minimaalpolünoom.

Näide 2.8.3. Leida maatriksite

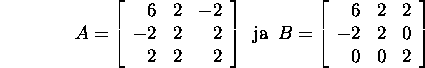
karakteristlikud ja minimaalpolünoomid. Leiame esmalt karakteristlikud polünoomid:

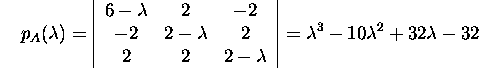
ja

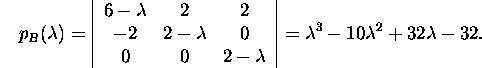
Seejärel leiame minimaalpolünoomid:

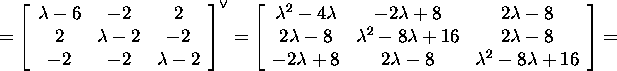
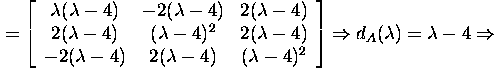
ja

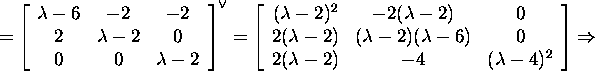
Ülesanne 2.8.2.^* Leidke maatriksi A minimaalpolünoom, kui

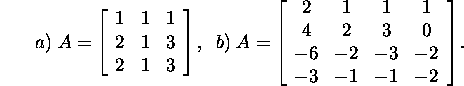
Peatüki algus: Maatriksid
Eelmine: Maatriksi normid ja konditsiooniarvud
Järgmine: Maatr iksargumendiga funktsioonid