Givens QR Factorization

Next we consider how to use the Givens rotations to compute the QR factorization of a given matrix.

Example 2.4.1. Consider for the idea of the Givens QR factorization:





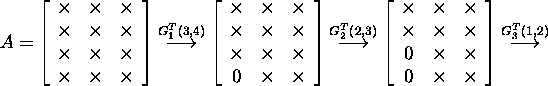
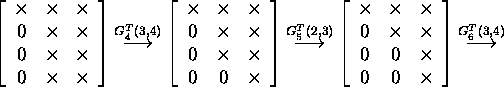
The orthogonal matrix has the form:

Example 2.4.2.^* Find the Givens QR factorization of


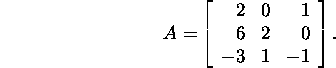
Let us annihilate the element A(3,1) of A. For this we construct the Givens matrix G₁(2,3). Find the values c and s:

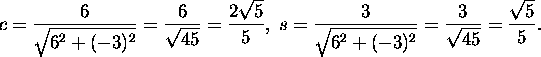
Thus, we have

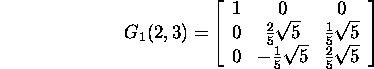
and



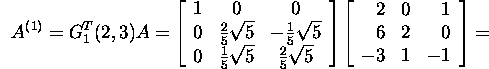
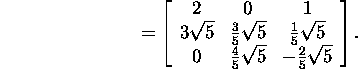
For the annihilation of the element A⁽¹⁾(2,1) of A⁽¹⁾ we construct the Givens matrix G₂(1,2). Find the values c and s:

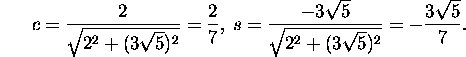
Thus,

and



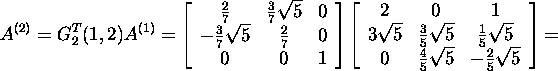
To annihilate the element A⁽²⁾(3,2) of A⁽²⁾ we construct the Givens matrix G₃(2,3). Find the values of c and s:

and

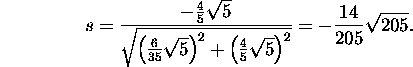
Thus,

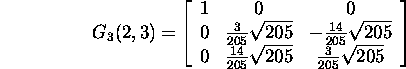
and

:

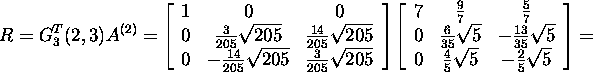
and





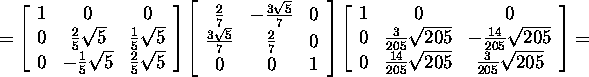
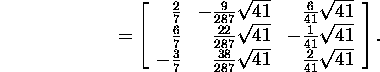
Let us check:



:

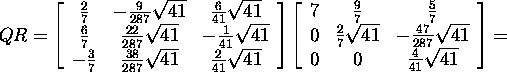
Exercise 2.4.1. Find the Givens QR factorization of the matrix A in example 2.3.2.

Exercise 2.4.2.^* Find the Givens QR factorization of A if