Definition
2.1.1. If 
and 
then the matrix of the form
is called the Householder matrix or Householder reflection and
the vector 
is called the Householder vector.
Proposition 2.1.1.
The Householder matrix H is symmetric
and orthogonal. The Householder
reflection reflects every vector 
in the hyperplane 
.
Proof. Indeed,
and
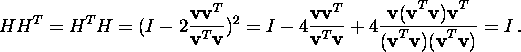
To prove the third part of the assertion, we choose on the hyperplane
an orthogonal basis
Hence, 
(i=
1:
)
and 
=1:
.
If
then
i.e., the vectors 
and 
have onto the hyperplane
the same orthogonal projection
but projections onto the vector
have opposite directions. Thus
is the reflection of
in the hyperplane .
It is significant to note that the Householder
matrix H depends only on the direction of Householder
vektor
and does not depend on the sign of the direction and length of .
Proposition 2.1.2.
If 
and 
then vector ,
where H is the Householder matrix
denoted by (1), has the same direction as 
,
i.e., the Householder reflection H
applied to the vector
annihilates all but the first component of the vector .
Proof. Our aim is to determine for a nonzero vector
the Householder vector
so that 
Since
and 
then 
By choosing 
we obtain that
and
Choose 
so that in the latter representation of
the coefficient of
is zero, i.e.,
For this choice
we have 
and
Example 2.1.1 Let 
Find the Householder vector
and according to it the Householder transformation that annihilates the
two last coordinates of the vector .
By Proposition 2.1.1 we compute 
Choose the sign plus for coefficient of
and we obtain 
Find the Householder matrix H that
depends only on direction of ,
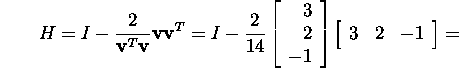
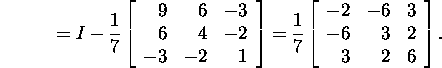
Check,
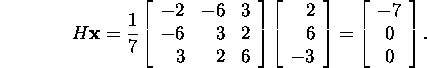
Exercise 2..1.1.* Find the Householder
matrix H such that 
,
where 
Let 
(
=1:
)
be the Householder matrices. Consider
the product of these matrices
where
and each 
has the form
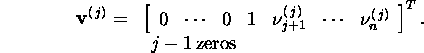
The matrix Q can be written in the form
where W and Y are 
matrices.
The answer to the question how to find representation (2)
is given with the following proposition.
Proposition 2.1.3. Suppose
is an orthogonal matrix with 
If 
where
and 
then
where 
and 
and consequently, W+, 
Proof. Since
and
then 
and the assertion of the proposition holds.