Decomposition of the System Matrix and Convergence of the Iterative process

Both Jacobi's and the Gauss-Seidel algorithms are of the type
 
where A=M-N. Herewith is said that the decomposition of the matrix A is given. Applying the iterative algorithm, it is important that the linear system (6) with the system matrix M were easy to solve. By Jacobi's method M is a diagonal matrix and by the Gauss-Seidel method it is a lower triangular matrix. It appears that the convergence of the iterative process given by (6) depends on the spectral radius of the matrix M^-1N.

Definition 7.3.1. The quantity

is the spectral radius of the matrix .

Proposition 7.3.1. Let A=M-N be the decomposition of the regular matrix and let If the matrix M is regular and
 
then the sequence of the approximation defined by algorithm (6) converges to the solution of system (1) by arbitrary initial approximation .

Proof. Let us get
 
Since the exact solution satisfies the equality
 
then from equalities (6) and (9) we get

Taking into account (8), we find for arbitrary non-negative integer k the relation

or

In virtue of proposition 7.1.2, it follows from inequality (7) that

Thus,

Example 7.3.1.^* Let the matrix of the system be

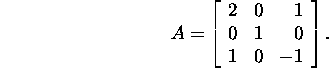
We will prove that the sequence of the approximations defined by Jacobi's algorithm converges to the solution of the system for any initial approximation .
Since



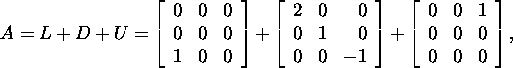
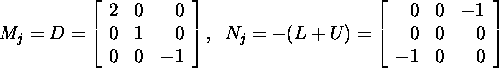
and

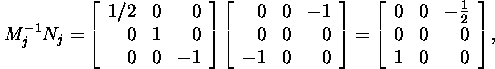
then

and

We note that the matrix A is regular. Hence, in virtue of proposition 7.3.1, the sequence of the approximations defined by Jacobi's algorithm converges to the solution of the system for any initial approximation .

Problem 7.3.1.^* Solve the system

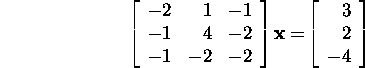
both by Jacobi's and the Gauss-Seidel method. Prove that the sequences of the approximations defined by these algorithms converge to the solution of this system for any initial approximation .

Problem 7.3.2.^* Solve the system

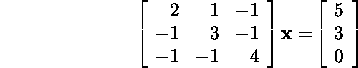
both by Jacobi's and the Gauss-Seidel method. Prove that the sequences of the approximations defined by these algorithms converge to the solution of this system for arbitrary initial approximation .

Definition 7.3.2. The matrix is a matrix with the strictly dominant diagonal if

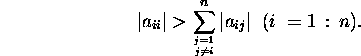
Remark 7.3.1. If the matrix is a matrix with the strictly dominant diagonal, then the spectral radius of the matrix M_J^-1N_J satisfies the condition

i.e., the iteration given by formula (4) converges.

Proof. See Golub, Loan (1996, pp. 120, 512). \

Proposition 7.3.2. If is a symmetric positive definite matrix, then the Gauss-Seidel iterative process converges for arbitrary .

Proof. Let us denote A=L+D+L^T, where L is a strictly lower triangular matrix (zeros on the leading diagonal) and D is a diagonal matrix. Since the matrix A is positive definite, then, in virtue of corollary 6.2.1, the matrix D is also positive definite. Hence it exists The matrices A and L+D are regular. Therefore, in virtue of proposition 7.3.1, to prove the convergence of the Gauss-Seidel iterative process, it is sufficient to show that the spectral radius of the matrix G=-(L+D)^-1U satisfies the condition Let G₁=D^1/2GD^-1/2. Since the similar matrices G and G₁ have the same spectrum, then it is sufficient to check the condition . Let L₁=D^-1/2LD^-1/2. We find that







Hence it is sufficient to prove that If while , then



and

and

If we set then and

and also

Thus,
 
Since, the matrix A is positive definite, then, in virtue of proposition 6.2.1, the matrix D^-1/2AD^-1/2 is also positive definite and





Hence



and condition (10) implies i.e.,