Acceleration of the Convergence of an Iterative Process

If the quantity is smaller than one but close to one, then the Gauss-Seidel method converges but very slowly. It arises a problem, how to accelerate the convergence of the sequence of approximations ? One of the ways of acceleration of the convergence is the so-called method of relaxation. The relaxation method is based on the algorithm

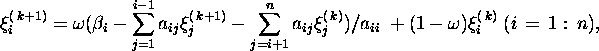
which can be written in the matrix form

where and The problem lies in finding the parameter so that were the least. By certain additional conditions, this problem can be solved.

The second way of acceleration of the convergence is the so-called Chebyshev method of convergence acceleration. Let us suppose that we have found using algorithm (6), the approximations of the solution of system (1). Let
 
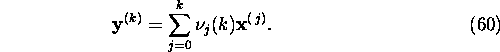
The problem lies in finding the coefficients in formula (11) so that the error vector of the approximation were smaller than the error vector In case of

it is natural to demand that This is just a case when
 
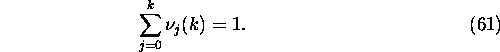
Hoe to choose the factors so that they would satisfy (12), and the error vector were the shortest? Since

then



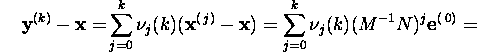
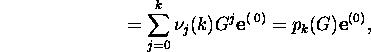
where G=M^-1N and

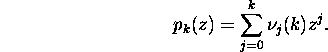
From condition (12), it follows that p_k(1)=1. In addition,
 
We confine ourselves further to the case of a symmetric matrix G. Let the eigenvalues of the symmetric matrix G satisfy the chain of inequalities

If is the eigenvalue corresponding to the eigenvector , then

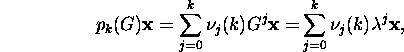
i.e., the vector is also the eigenvector of the matrix p_k(G) corresponding to the eigenvalue

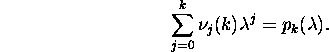
In case of the symmetric matrix G, the matrix p_k(G) is also symmetric. Hence

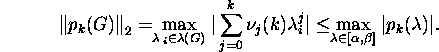
To decrease the quantity one must find such a polynomial p_k(z) that has small values on the segment and satisfies the condition p_k(1)=1. The Chebyshev polynomials have these properties. The Chebyshev polynomials are defined on the segment [-1;1] by the recurrence relation

while c₀(z)=1 and c₁(z)=z. These polynomials satisfy the inequality

and c_j(1)=1, and the values |c_j(z)| grow quickly outside the segment [-1;1]. The polynomial
 
where

satisfies the conditions p_k(1)=1 and

Taking into account relations (13) and (14), we find

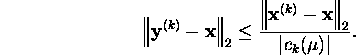
Therefore, the greater is the greater is , and the greater will be the Chebyshev'i acceleration.