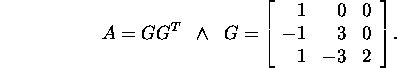Positive Definite Systems

Definition 6.2.1. The matrix is a positive definite matrix if

for all nonzero vector .

Example 6.2.1. The matrix

is a positive definite one since for

Problem 6.2.1.^* Show that the matrix

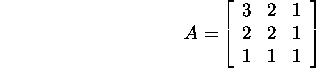
is positive definite.

Proposition 6.2.1. If is a positive definite matrix and the column vectors of the matrix are linearly independent, then the matrix

is also positive definite.

Proof. If for the vector it holds the relation

then

and from the positive definiteness of the matrix A it follows that Since the column vectors of the matrix X are linearly independent, then from it follows that Hence from conditions and it follows that i.e., the matrix B is positive definite.

Corollary 6.2.1. If the matrix is positive definite, then all the submatrices of the matrix A obtained by deleting the rows and columns of the matrix A with the same numbers are positive definite and all the elements on the leading diagonal of the matrix are positive.

Proof. If is a vector with natural number coordinates satisfying the condition

then

is a matrix got from the unit matrix I_n by taking the column-vectors with indices Hence the column-vectors of the matrix X are linearly independent, and proposition 6.2.1 implies that the matrix X^TAX is positive definite. The matrix X^TAX is a submatrix of the matrix A obtained from the rows and columns with numbers of the matrix A. Therefore, all the submatrices of the matrix A obtained by deleting the rows and columns of the matrix A with the same numbers are positive definite. Taking k=1, we get the second part of the statement.

Corollary 6.2.2. If is positive definite, then the matrix A has a decomposition A=LDM^T and all the leading diagonal elements of the matrix D are positive.

Proof. On the ground of corollary 6.2.1, all the submatrices of the matrix A are positive definite, and, therefore, regular matrices, and proposition 6.1.1 implies the existence of the LDM^T decomposition. Taking X=L^-T in proposition 6.2.1, we find that the matrix

is positive definite. Since the matrix M^TL^-T is an upper triangular matrix with the unit diagonal, the matrices B and D have the same leading diagonal and the elements on it must be positive, provided that B is positive definite.

Proposition 6.2.2 (Cholesky factorization). If the matrix is symmetric and positive definite, then there exists exactly one lower triangular matrix G with the positive leading diagonal such that
 

Proof. In virtue of proposition 6.1.2, there exist and are uniquely defined the lower triangular matrix L with the unit diagonal and the diagonal matrix such that it holds the decomposition (3), i.e., A=LDL^T. The corollary 6.2.2 provides that elements d_k of the matrix D are positive. Therefore, the matrix

is a lower triangular matrix with the positive leading diagonal, and equality (5) holds. The uniqueness of the the factorization follows from the uniqueness of the decomposition (3).

The factorization (5) is known as the Cholesky factorization. The matrix G is called the Cholesky triangular matrix of the matrix A. To solve the system of equations

having the symmetric and positive definite matrix A, one has to find the Cholesky triangular matrix of the matrix A. Secondly, one has to solve the system with the triangular matrix

Thirdly, one has to solve the system

The Cholesky factorization can be found step by step.

Proposition 6.2.3. If the matrix is symmetric and positive definite, then, denoting

the matrix A can be expressed by
 
where The matrix is positive definite. If

then A=GG^T, where

Proof. Let us check the accurancy of the decomposition (6):





If

then



Since the matrix A is positive definite and the column-vector system of the matrix X is linearly independent, proposition 6.2.1 implies the positive definiteness of the matrix

and from corollary 6.2.1 it follows that the matrix is linewise positive definite. So we can, analogously to the partition of the matrix A into blocks, decompose also the matrix into blocks, etc.

Example 6.2.2. Let us find the LU, LDM^T, LDL^T and Cholesky factorizations of the matrix

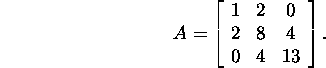
The principal minors of the matrix A are nonzero. We find

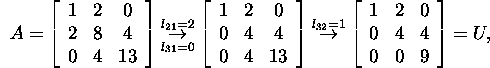
and

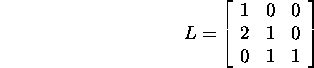
and also

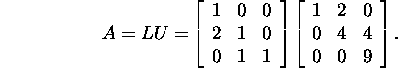
Knowing the LU factorization of the matrix A, we will find the LDM^T decomposition, LDL^T decomposition and Cholesky factorization of it:

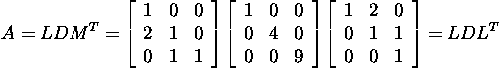
and

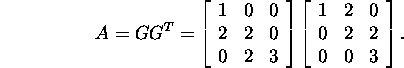
Let us find the Cholesky factorization of the matrix A also step by step using the algorithm given in proposition 6.2.3. Since on the first step

then

On the next step,

and

Therefore,

and

and

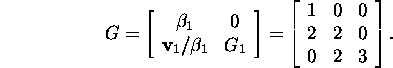
Problem 6.2.2.^* Find the Cholesky factorization of the positive definite matrix

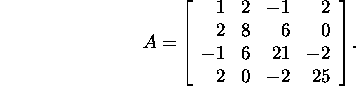
Problem 6.2.3.^* Solve the system of equations where

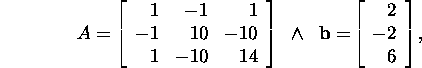
when the Cholesky factorization of the matrix A is given