Powers of a Matrix and Inverse Matrix

Proposition 7.1.1. If and then I-F is a regular matrix and

while

Proof. If we suppose the contrary to the assertion that the matrix I-F is singular, then there exists such a nonzero vector that i.e., and , Hence the matrix I-F is a regular matrix. To find the matrix (I-F)^-1, we consider the identity

Since

then

that implies

and

which was to be proved.

Proposition 7.1.2. Let Q^HAQ=T=D+N be the Schur factorization of the matrix , while D is a diagonal matrix and N is a strictly upper triangular matrix (on the leading diagonal there are zeros). Let and be respectively the greatest and the least by modulus eigenvalues of the matrix A. If then for all

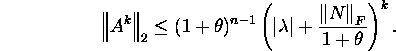
If A is a regular matrix and the number is such that

then for all

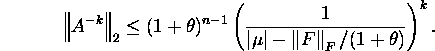
Proof. See Golub, Loan (1996, pp 336-337).

The formula

which is easily checked shows how the inverse matrix changes when the matrix A is substituted by the matrix B. The modification of this formula is a formula of Sherman-Morrison-Woodbury given in the following proposition.

Proposition 7.1.3. If and while matrices A and I+V^TA^-1U are regular,

Proof. See Golub, Loan (1996, pp. 50).