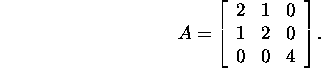Polar Decomposition of a Matrix and Method of Square Roots

Proposition 6.4.1 (on the reduced singular value decomposition of a matrix). If the matrix has the singular value decomposition where and are orthogonal matrices and then the reduced singular value decomposition of this matrix A is

where U₁=U(: ,1:n) and :).

Proof. If one uses the representation of the matrices U and V by the column-vectors

and

then



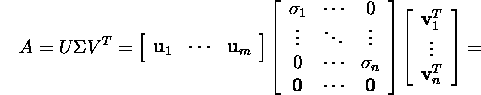
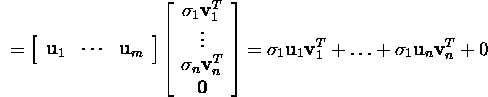
and

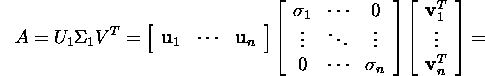
Example 6.4.1. Find the reduced singular value decomposition of the matrix

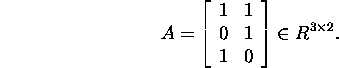
The singular value decomposition of the matrix A was found in example 3.3.1. It is

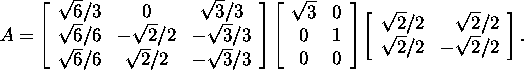
According to proposition 6.4.1, the reduced singular value decomposition has the form

where U₁=U(: ,1:n) and :), i.e.,

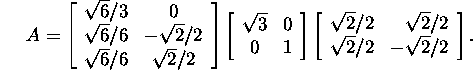
Proposition 6.4.2. If the matrix has the reduced singular value decomposition

then the matrix A can be given in the form
 
where is a matrix with orthogonal columns and is a symmetric positive semidefinite matrix.

Proof. Since then

Let us check the correctness of the assertion of the proposition. Firstly, Z is a matrix with orthonormal columns since

Secondly, is a positive semidefinite matrix since

where

Definition 6.4.1. The factorization of the matrix in the form (12) is called the polar decomposition.

Example 6.4.2. Find the polar decomposition of the matrix

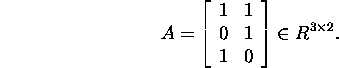
In example 6.4.1 the reduced singular value decomposition of the matrix A was found. Let us find the factors Z and P occuring in the polar decomposition of the matrix A:







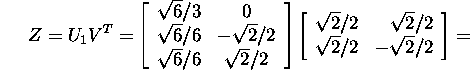
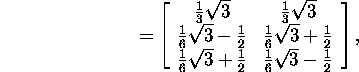
Hence the polar decomposition of the matrix A is

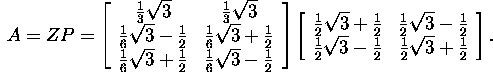
Problem 6.4.1.^* Find the polar decomposition of the matrix

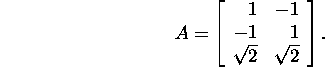
Definition 6.4.2. Let If the matrix satisfies the equation X²=A, then the matrix X is the square root of the matrix A.

Proposition 6.4.3. If

is the Cholesky factorization of the symmetric positive semidefinite matrix and

is the singular value decomposition of the matrix G and

then

i.e., the matrix X is the square root of the matrix A, where X is a symmetric positive semidefinite matrix. Only one such X exists.

Proof. We find



Show that the matrix X is a uniquely defined symmetric positive semidefinite matrix!

Example 6.4.3. Let us find the square root of the matrix

The matrix A is symmetric and positive semidefinite (see example 6.3.1), and

Since

then

Problem 6.4.2.^* Find the square root of the matrix