Positive Semidefinite Matrices

Definition 6.3.1. A matrix is called a positive semidefinite matrix if

Example 6.3.1. The matrix

is positive semidefinite since for korral



and in the case we see that but i.e., the matrix A is a positive semidefinite matrix, but it is not positive definite.

Problem 6.3.1.^* Show that the matrix

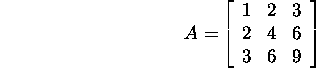
is positive semidefinite.

Proposition 6.3.1. If is a symmetric positive semidefinite matrix, then
 

 

 
and
 

Proof. Let and Since the matrix A is positive semidefinite and symmetric, then



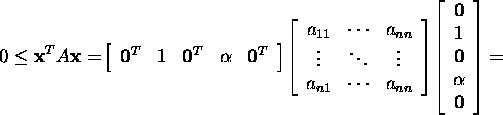
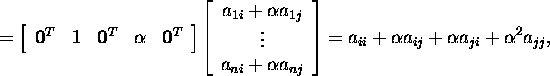
and
 
Condition (11) is satisfied exactly when

from which, in its turn, it follows (7), and from it (8). Fixing in inequality (11) and taking into consideration the symmetry of the matrix A, we get



and assertions (9) and (10).

Problem 6.3.2. Show that the algorithm of the Cholesky factorization A=GG^T is applicable (with the small changes) also to the symmetric positive semidefinite matrix A.