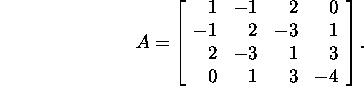LDM^T Decomposition and LDL^T Decomposition of a Matrix

Next we will consider the special cases of LU factorizations of square matrices.

Proposition 6.1.1. If all the principal minors of the matrix are different from zero, then there exist such lower triangular matrices L and M with the unit leading diagonal and a diagonal matrix that
 
and the decomposition (1) is unique.

Proof. Since all the principal minors of the matrix are nonzero, then the proposition 1.2.2 implies that there exists the unique LU factorization of the matrix A
 
Let where d_i=u_ii (i =1: n). From the regularity of the matrix A it follows that the matrix D is regular. Therefore, and M^T=D^-1U is an upper triangular matrix. Hence

The uniqueness of the decomposition (1) follows from the uniqueness of the factorization (2).

Definition 6.1.1. The decomposition (1) is called the LDM^T decomposition of the regular matrix .

Example 6.1.1.^* Let us find the LDM^T decomposition of the matrix

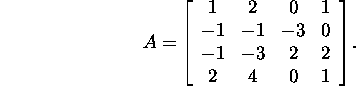
We state that if the principal minors of the matrix A are different from zero, then, by taking the matrix A to the triangular form by the Gauss transformation, we find simultaneously both the matrix L and the matrix U. Namely, the entry l_ij of the lower triangular matrix L equals the factor by which the j-th row must be multiplied when it is substracted from the i-th row to delete the entry in the i-th row. We find



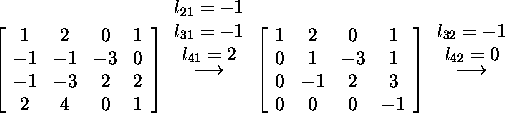
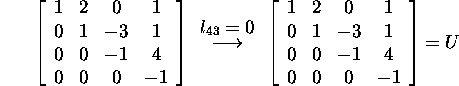
and

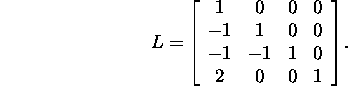
Let us check:

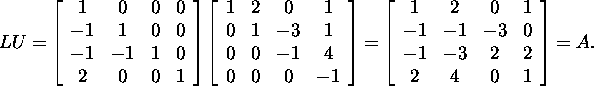
Proposition 6.1.2. If the regular matrix is symmetric and the LDM^T decomposition of it has the form (1), then L=M, i.e.,
 

Proof. From decomposition (1) it follows that

Multiplying both sides of the last equality on the left by matrix M^-1, we get
 
The matrix M^-1AM^-T is symmetric since

The matrix M^-1AM^-T is a lower triangular matrix since both M^-1 and AM^-T=LD are lower triangular matrices. In virtue of relation (4), the matrix M^-1LD is also symmetric and lower triangular. Therefore, the matrix M^-1LD is diagonal. Since the matrix D is regular, then also the matrix M^-1L is diagonal. In addition, the matrix M^-1L is a lower triangular matrix with the unit diagonal. Hence M^-1L=I or

Problem 6.1.1.^* Find the LU factorization, LDM^T decomposition and LDL^T decomposition of the matrix