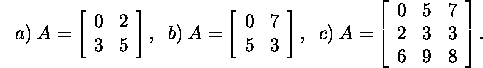Under certain conditions the system matrix A of
the equation 
can be expressed in the form of a product of a unit lower triangular
matrix L with units on the main diagonal and an upper triangular
matrix U,and as the result, one has to solve two systems with triangular
matrices.
Proposition
1.2.1 (LU-method). If 
where L is unit lower triangular, U is regular upper triangular
and 
then 
and for the solution of the system one has first to solve the system 
and then the system 
Example 1.2.1. Solve the system
using LU-method. Since
then, by Proposition 1.2.1, we have to solve
first the system
The solution of this system is 
and 
Second, solving the system
we find that 
and 
Thus, 
The Gaussian elimination considered in the main course
of linear algebra for solution of systems of linear equations is applicable
also to the LU-factorization. Let 
where 
If
and
then
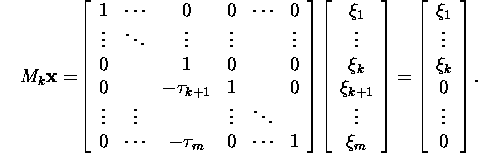
Definition
1.2.1. A matrix Mk of the form (2) is called a Gauss
matrix, the components 
are called Gauss multipliers, and the vector 
is called the Gauss vector. The transformation defined with the
Gauss matrix 
is
called the Gauss transformation.
Definition 1.2.2.
The value
is called the k-th pivot of the matrix 
where 
and 
If 
then for the nonzero pivots of A the Gauss
matrices 
can be found such that 
is upper triangular.
Example 1.2.2. Let us consider the finding of the
Gauss matrices M1 ja 
and
the upper triangular matrix U for
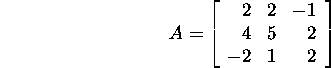
By relation (2), we obtain that
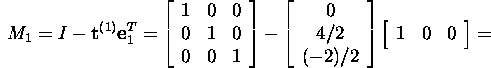
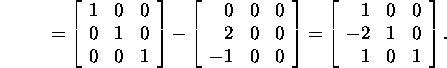
Thus,
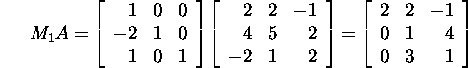
and
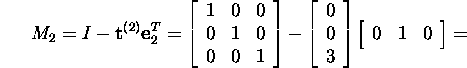
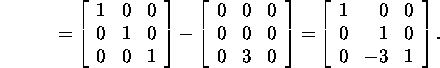
Therefore,
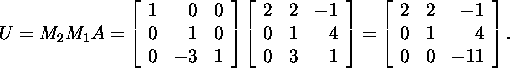
Note that matrix 
is upper triangular in columns 1 to k-1, and for the calculation
of the elements of the Gauss matrix Mk
is used the matrix vector A(k-1)(k:m,k).
The calculation of Mk is possible if 
.
Moreover, 
If to choose
then
We stress that in our treatment the lower triangular matrix L is
a unit lower triangular matrix.
Proposition 1.2.2. If
1:k,1:
for (k=1:n-1),then 
has an LU factorization. If the LU
factorization exists and A is regular, then the LU
factorization is unique and 
Proof. Suppose k-1 steps have been taken
and the matrix
has been found. The element akk(k-1)
is the k-th pivot of A and
1:k,1:
Hence, if A(1:k,1:k) is regular, then
and A has an LU factorization. Let
us suppose that regular matrix A has two LU
factorizations A=L1U1 and
A=L2U2. We have L1U1=L2U2
or L2-1L1=U2U1-1.
Since L2-1L1 is unit lower
triangular and U2U1-1is
upper triangular, then L2-1L1=I
, U2U1-1=I and L2=L1
and also U2=U1.
Example 1.2.3.* Find the LU
factorization of the matrix
Find the Gauss matrix M1 for
A :
Thus,
and
Example 1.2.4.* Find the LU
factorization of
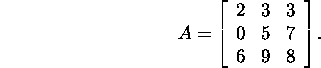
Find the Gauss matrix M1 for
A:
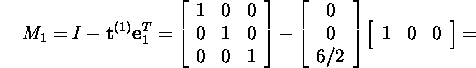
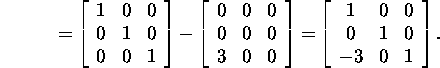
Thus,
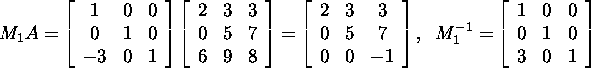
and since M1A is upper triangular, then M2=I
and
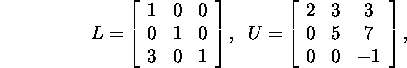
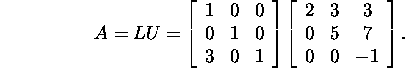
Example 1.2.5.* By using the
LU factorization, solve the system ,
where
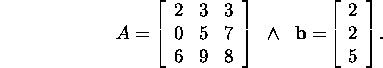
In example 1.2.4 there has been found the LU
factorization for A:
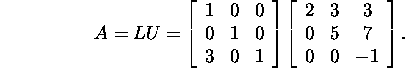
By solving the system
, i.e.,
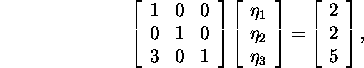
we obtain that
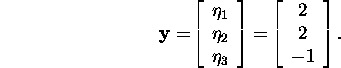
By solving the system 
, i.e.,
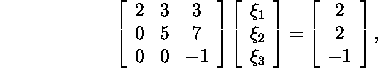
we obtain that
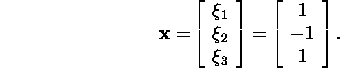
Exercise 1.2.1.* Find the LU
factorization of A if
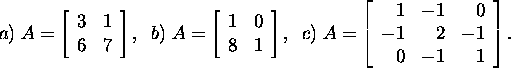
Exercise 1.2.2.* By using the LU
factorization solve the system ,
where
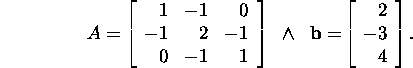
If the principal minors of a rectangular matrix 
are nonzero, i.e.,
then A has an LU factorization.
Example 1.2.6. The following equalities hold:
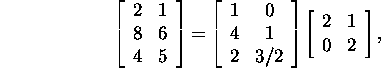
As it is known from the main course of algebra, the direct
application of the Gaussian elimination, therefore also the direct realization
of the LU factorization, fails if at least
one of the principal minors is singular. It turns out that for a regular
matrix it is possible after an appropriate interchange of matrix rows to
find the LU factotization. Permutation
matrices are used for interchanging the matrix rows (columns).
Definition 1.2.3. A
permutation matrix 
is the identity I with its rows reordered.
Example 1.2.7. Consider the effect of multiplying
of a 
matrix A by concrete permutation matrix P.
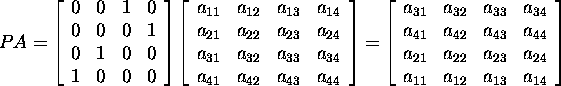
Multiplying by the permutation matrix P
on the left,, we obtain a new matrix, where the rows of initial the matrix
are reordered exactly in the same way as the rows of the identity I
are reordered for getteing P. Multiplying on the right,
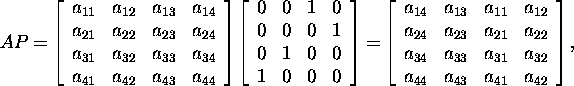
we obtain a new matrix, where the columns of the initial matrix are reordered
in the same way as the columns of the identity I are reordered for
getting P . It holds
Proposition 1.2.3.
If 
and 
then there exists a permutation matrix
such that all the principal minors of PA are nonzero, and consequently,
there exists the LU factorization
Example 1.2.8.* Let
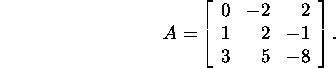
Find for a certain permutation matrix
the LU factorization of PA.
Interchange the first and second rows of A, i.e., choose
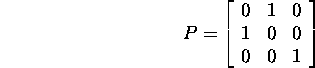
and find for the matrix
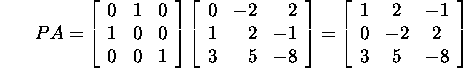
the Gauss matrix
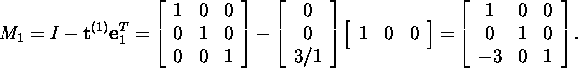
Thus,
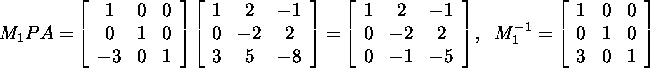
and
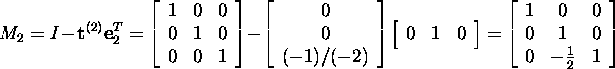
and
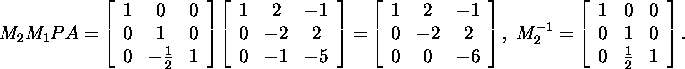
Consequently,
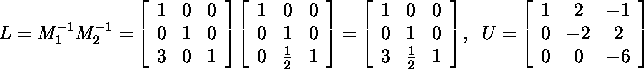
and
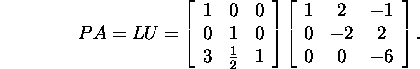
Exercise 1.2.3.* Find for a certain
permutation matrix P the LU
factorization of PA if
