One of the fundamental concepts of linear algebra is the concept of vector space. At the same time it is one of the more often used concepts algebraic structure in modern mathematics. For example, many function sets studied in mathematical analysis are with respect to their algebraic properties vector spaces. In analysis the notion ``linear space'' is used unstead of the notion ``vector space''.
Definition 1.1.1 A
set 
is called a vector space over the number
field 
if to every pair 
of elements of
there corresponds a sum 
,
and to every pair 
where 
and 
,
there corresponds an element 
,
with the properties 1-8:
1. 
(commutability of addition);
2. 
(associativity of addition);
3. 
(existence of null element);
4. 
(existence of the inverse element);
5. 
(unitarism);
6. 
(associativity with respect to number multiplication);
7. 
(distributivity with respect to vector additism);
8. 
(distributivity with respect to number additism).
The properties 1-8 are called the vector
space axioms. Axioms 1-4 shows that
is a commutative group or an Abelian group with respect to vector addition.
The second correspondence is called multiplication of the vector by a number,
and it satisfies axioms 5-8. Elements of a vector
space are called vectors. If 
,
then one speaks of a real vector space, and if
,
then of a complex vector space. Instead of
the notion ``vector space'' we shall use the abbreviative ``space''.
Example 1.1.1. Let us consider the set of all 
matrices
with real elements:
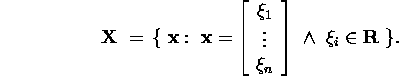
The sum of two matrices we define in usual way by the addition of the corresponding
elements. By multiplying the matrix by a real number 
we multiply all elements of the matrix by this number. The simple check
will show that conditions 1-8 are satisfied. For example,
let us check conditions 3 and 4. We construct
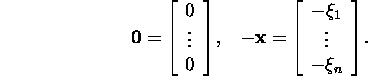
As
the element 
satisfied condition 3 for arbitrary ,
and thus it is the null element of the space .
For the element 
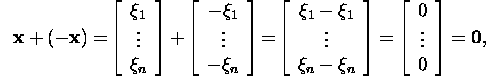
i.e., condition 4 is satisfied. Make sure of the valitidy of the remaining
conditions 1-2 and 5-8.
The vector space in example 1.1.1 is called n-dimensional
real arithmetical space or in short space 
.
Declaring the vector 
of the space
we often use the transposed matrix
In this presentation we often use punctuation mark (comma, semicolon) to
separate the components of the vector, for example
Example 1.1.1.* Let U,
be a set that consists of all pairs of real numbers 
We
define addition and multiplication by scalar in U as follows:
Is the set U a vector space?
Proposition 1.1.1. Let
be a vector space. For arbitrary vectors 
and number 
the following assertions and equalities are valid:
of the vector space
is unique; 
of each
is unique; 
Become convinced of the trueness of these assertions!
Example 1.1.2. Let us consider the set of all 
matrices
with complex elements. The sum of this matrices will be defined by the
addition of the corresponding elements of the matrices. By multiplying
the matrix by a complex number
one will multiply by this number all the elements of the matrix. We leave
the check that all conditions 1-8 are satisfied to the
reader. This vector space over the complex number field 
will be denoted 
If we confine ourselves to real matrices, then we shall get vector
space 
over the number field 
The space 
will be identified with the space 
and the space 
with the space 
Example 1.1.3. The set 
of all functions 
is a vector space (prove!) over the number field 
if
and
