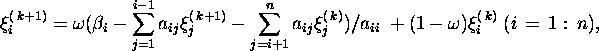
mille maatrikskujuks on
kus
Peatüki
algus: Võrrandisüsteemide
lahendamine iteratsioonimeetodil
Eelmine: Süsteemimaatriksi
lagu ja iteratsiooniprotsessi koonduvus
Järgmine: Numbriline stabiilsus
Kui suurus ![]() on ühest väiksem, kuid ühele lähedane suurus, siis
Gauss-Seideli meetod koondub,
kuid väga aeglaselt. Tekib probleem, kuidas lähendite jada
on ühest väiksem, kuid ühele lähedane suurus, siis
Gauss-Seideli meetod koondub,
kuid väga aeglaselt. Tekib probleem, kuidas lähendite jada ![]() koonduvust kiirendada? Üheks koonduvuse kiirendamise võtteks
on nn relaksatsioonimeetod. Relaksatsioonimeetodi
aluseks on algoritm
koonduvust kiirendada? Üheks koonduvuse kiirendamise võtteks
on nn relaksatsioonimeetod. Relaksatsioonimeetodi
aluseks on algoritm
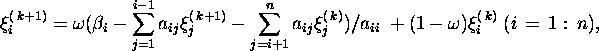
mille maatrikskujuks on
![]()
kus ![]() ja
ja ![]() Probleemiks on määrata relaksatsiooniparameeter
Probleemiks on määrata relaksatsiooniparameeter ![]() nii, et
nii, et ![]() oleks vähim. Teatud lisatingimustel on see probleem lahendatud.
oleks vähim. Teatud lisatingimustel on see probleem lahendatud.
Koonduvuse kiirendamise Chebyshev'i
võte.
Oletame, et oleme leidnud algoritmi (6)
abil süsteemi (1) lahendi ![]() lähendid
lähendid ![]() Olgu
Olgu
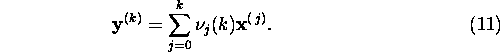
Probleemiks on määrata valemis (11) kordajad
![]() selliselt, et lähendi
selliselt, et lähendi ![]() veavektor
veavektor ![]() oleks väiksem kui veavektor
oleks väiksem kui veavektor ![]() Juhul
Juhul
![]()
on loomulik nõuda, et ![]() See on parajasti siis nii, kui
See on parajasti siis nii, kui
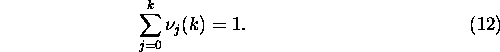
Kuidas valida kordajad ![]() nii, et need rahuldaks seost (12) ja veavektor oleks
lühima pikkusega? Kuna
nii, et need rahuldaks seost (12) ja veavektor oleks
lühima pikkusega? Kuna
![]()
siis
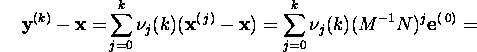
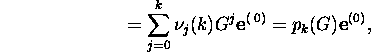
kus G=M-1N ja
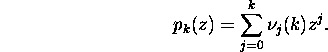
Tingimusest (12) järeldub, et pk(1)=1.
Lisaks,
![]()
Piirdume järgnevas vaid sümmeetrilise maatriksi G juhuga.
Rahuldagu sümmeetrilise maatriksi G omaväärtused
![]() võrratuste ahelat
võrratuste ahelat
![]()
Kui ![]() on maatriksi G omaväärtus,
mis vastab omavektorile
on maatriksi G omaväärtus,
mis vastab omavektorile
![]() ,
siis
,
siis
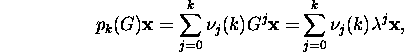
st vektor ![]() on ka maatriksi pk(G) omavektor,
mis vastab omaväärtusele
on ka maatriksi pk(G) omavektor,
mis vastab omaväärtusele
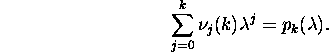
Sümmeetrilise maatriksi G korral on sümmeetriline
ka maatriks pk(G). Järelikult,
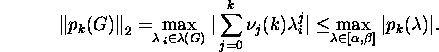
Selleks, et vähendada suurust ![]() ,
on vaja leida selline polünoom pk(z), mille
väärtused lõigul
,
on vaja leida selline polünoom pk(z), mille
väärtused lõigul ![]() on väikesed ja mis rahuldab tingimust pk( 1)=1.
Sellise omadusega on Chebyshev'i polünoomid. Chebyshev'i
polünoomid lõigul [-1;1] defineeritakse rekurrentse seosega
on väikesed ja mis rahuldab tingimust pk( 1)=1.
Sellise omadusega on Chebyshev'i polünoomid. Chebyshev'i
polünoomid lõigul [-1;1] defineeritakse rekurrentse seosega
![]()
kusjuures c0(z)=1 ja c1(z)=z.
Need polünoomid rahuldavad võrratust
![]()
ja cj(1)=1 ning suurused |cj(z)|
kasvavad kiiresti väljaspool lõiku [-1;1]. Polünoom
![]()
kus
![]()
rahuldab tingimusi pk(1)=1 ja
![]()
Arvestades seoseid (13) ja(14), leiame, et
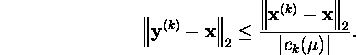
Järelikult, mida suurem on ![]() seda suurem on
seda suurem on ![]() ja seda suurem on Chebyshev'i kiirendus.
ja seda suurem on Chebyshev'i kiirendus.