Peatüki algus: Võrrandisüsteemide lahendamine iteratsioonimeetodil
Eelmine: Maatriksi astmed ja pöördmaatriks
Järgmine: Süsteemimaatriksi lagu ja iteratsiooniprotsessi

Olgu ja (i =1:n). Vaatleme võrrandisüsteemi
 
lahendamist iteratsioonimeetodil.

Definitsioon 7.2.1. Süsteemi (1) lahendi lähendiks ehk lähisväärtuseks nimetatakse vektorit, mis teatavas mõttes erineb vähe vektorist Esitame süsteemi (1) kujul

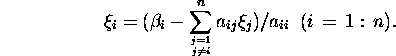
Jacobi iteratsiooniprotsess on defineeritud algoritmi
 
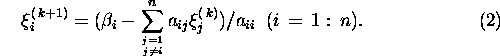
abil. Gauss-Seideli iteratsiooniprotsess on defineeritud algoritmi
 
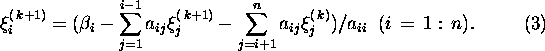
abil. Nii Jacobi kui ka Gauss-Seideli iteratsiooniprotsessi korral saab üleminekut süsteemi (1) lahendi lähendilt järgmisele lähendile kirjeldada, kasutades maatrikseid

ja kusjuures A=L+D+U. Näiteks, Jacobi algoritm (2) on esitatav kujul
 
kus M_J=D ja N_J=-(L+U). Gauss-Seideli algoritm (3) on esitatav kujul
 
kus M_G=D+L ja N_G=-U.

Näide 7.2.1.^* Lahendame süsteemi kus

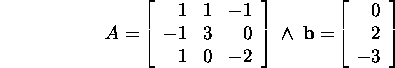
Jacobi meetodil.
Esitame maatriksi A kujul

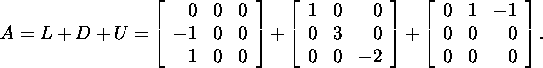
Moodustame maatriksid M_j ja N_j:

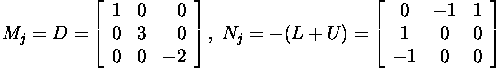
Jacobi iteratsiooniprotsessi algoritm on esitatav kujul

Kuna

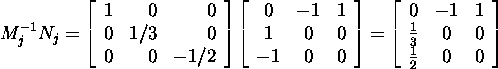
ja

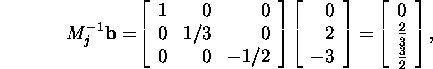
siis

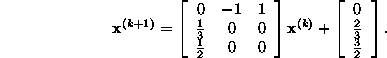
Kui valida alglähendiks siis saame









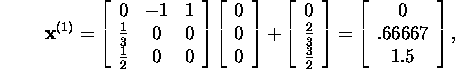
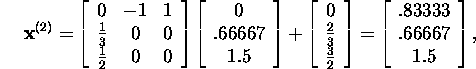
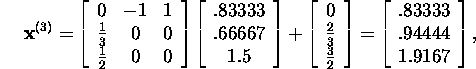
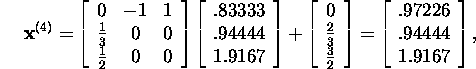
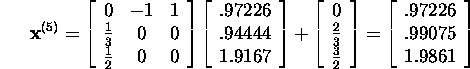
ja nii edasi (selle võrrandi täpne lahend on ).

Ülesanne 7.2.1.^* Lahendage näites 7.2.1 esitatud süsteem Gauss-Seideli meetodiga.