Peatüki algus: Võrrandisüsteemide lahendamine iteratsioonimeetodil
Eelmine: Võrrandisüsteemide lahendamine iteratsioonimeetodil
Järgmine: Jacobi meetod ja Gauss-Seideli

Lause 7.1.1. Kui ja siis I-F on regulaarmaatriks ja

kusjuures

Tõestus. Kui eeldame väitevastaselt, et maatriks I-F on singulaarne, siis leidub selline nullist erinev vektor et st ja ||x||_p=||Fx||_p ning Järelikult, maatriks I-F on regulaarmaatriks. Maatriksi (I-F)^-1 leidmiseks vaatleme samasust

Kuna

siis

millest järeldub, et

ja

mida oligi vaja tõestada.

Lause 7.1.2. Olgu Q^HAQ=T=D+N maatriksi Schuri lahutus, kusjuures D on diagonaalmaatriks ja N on rangelt ülemine kolmnurkmaatriks (peadiagonaalil nullid). Olgu ja maatriksi A mooduli poolest vastavalt suurim ja vähim omaväärtus. Kui arv 0, siis iga korral

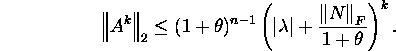
Kui A on regulaarmaatriks ja arv on selline, et

siis iga korral

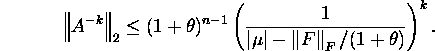
Tõestus. Vaadake Golub, Loan (1996, lk 336-337).

Lihtsalt kontrollitav valem

näitab, kuidas muutub pöördmaatriks, kui asendada maatriks A maatriksiga B. Selle valemi modifikatsiooniks on järgmise lausega esitatav Sherman-Morrison-Woodbury valem.

Lause 7.1.3. Kui ja kusjuures maatriksid A ja I+V^TA^-1U on regulaarsed, siis

Tõestus. Vaadake Golub, Loan (1996, lk 50).