Peatüki algus: Vektorid
Eelmine: Vektorid
Järgmine: Vektorruumi alamruumid

Lineaaralgebra üheks põhimõisteks on vektorruumi mõiste. Ühtlasi on see üks sagedamini kasutatavaid algebralise struktuuri mõisteid tänapäeva matemaatikas. Näiteks, paljud matemaatilises analüüsis vaadeldavad funktsioonide hulgad on oma algebraliste omaduste poolest vektorruumid. Analüüsis pruugitakse termini ''vektorruum'' asemel terminit ''lineaarne ruum''.

Definitsioon 1.1.1. Hulka X nimetatakse vektorruumiks üle arvukorpuse K, kui hulga X elementide igale paarile (x, y) on vastavusse seatud summa x + y X, ja igale paarile (, x), kus K ning x X, on vastavusse seatud element x X, kusjuures on rahuldatud tingimused 1-8 :

1. x + y = y + x (liitmise kommutatiivsus);
2. x + (y + z) = (x + y) + z (liitmise assotsiatiivsus);
3. 0 X: 0 + x = x (nullelemendi olemasolu);
4. x X -x X: x + (-x) = 0 (vastandelemendi olemasolu);
5. 1x = x (unitaarsus);
6. (x) = ()x (assotsiatiivsus arvude korrutamise suhtes);
7. (x + y) = x + y (distributiivsus vektorite liitmise suhtes);
8. ( + )x = x + x (distributiivsus arvude liitmise suhtes).

Tingimused 1-8 kannavad vektorruumi aksioomide nime. Aksioomid 1-4 näitavad, et X on vektorite liitmise suhtes kommutatiivne rühm ehk Abeli rühm. Teist vastavust nimetatakse vektori arvuga korrutamise tehteks ja see rahuldab aksioome 5-8. Vektorruumi elemente nimetame vektoriteks. Kui K = R, siis kõneldakse reaalsest vektorruumist ja kui K = C, siis kompleksest vektorruumist. Termini ''vektorruum'' asemel kasutame ka lühendit ''ruum.''

Näide 1.1.1. Vaatleme kõigi reaalsete elementidega n1-maatriksite hulka

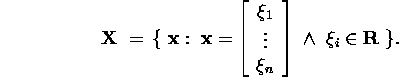
Kahe maatriksi summa defineerime tavalisel viisil, maatriksite vastavate elementide liitmise teel. Maatriksi korrutamisel reaalarvuga korrutame selle arvuga maatriksi kõik elemendid. Lihtne otsene kontroll näitab, et tingimused 1-8 on täidetud. Näiteks, kontrollime tingimusi 3 ja 4. Konstrueerime maatriksid

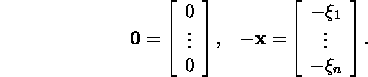
Kuna

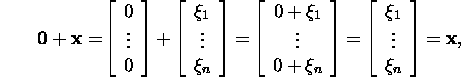
siis element rahuldab suvalise korral tingimust 3 ja on seega ruumi nullelement. Elemendi korral

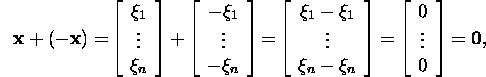
st tingimus 4 on täidetud. Veenduge, et ka ülejäänud tingimused (1-2 ja 5-8) on täidetud!

Näites 1.1.1 esitatud vektorruumi nimetatakse n-mõõtmeliseks reaalseks aritmeetiliseks ruumiks ehk lühidalt ruumiks . Ruumi vektori x kirjeldamisel kasutame tihti transponeeritud maatriksit

Viimases esituses pruugitakse sageli vektori komponentide eraldamiseks kirjavahemärke (koma, semikoolon), näiteks

Ülesanne 1.1.1.^* Olgu antud hulk U, mis koosneb kõikidest reaalarvupaaridest

Defineerime hulgal U liitmise ja skalaariga korrutamise järgmiselt:



Kas hulk U on vektorruum?

Lause 1.1.1. Olgu vektorruum. Mistahes vektorite ja arvu korral kehtivad järgmised väited ja võrdused:

• vektorruumi nullvektor on ainus;
• iga vastandvektor on ainus;
• vastandvektori ühesus lubab defineerida lahutamistehte seosega
  
  
• 
• 
• 
• 
• 

Veenduge nende väidete tõesuses!

Näide 1.1.2. Vaatleme kõigi kompleksarvuliste elementidega m  n-maatriksite hulka. Kahe maatriksi summa defineerime maatriksite vastavate elementide liitmise teel. Maatriksi korrutamisel kompleksarvuga korrutame selle arvuga maatriksi kõik elemendid. Lihtne kontroll, et tingimused 1-8 on täidetud, on jäetud lugejale. Saadud vektorruumi üle kompleksarvude korpuse tähistame Kui piirduda reaalarvuliste maatriksitega , siis saame vektorruumi üle arvukorpuse Ruum samastatakse ruumiga ja ruum ruumiga R^m.

Näide 1.1.3. Kõigi funktsioonide hulk on vektorruum (tõestage!) üle arvukorpuse , kui

ja

Peatüki algus: Vektorid
Eelmine: Vektorid
Järgmine: Vektorruumi alamruumid