Properties of Singular Value Decomposition

Relation (2) yields the relations
 
and
 

Proposition 3.2.1. If and
then for each = there hold the relations
 

 




and

Proof. Suppose n>m. Consider relation (3) that can be written in the form

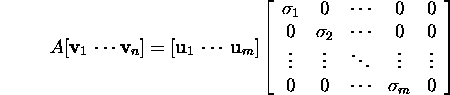
or

The latter is (5) for the elements in the m first columns of the matrix. Consider relation (4) that can be written in the form

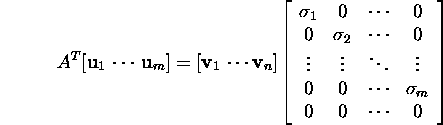
or

that represents relation (6) by elements. We note that ''0'' denotes also certain blocks consisting of zeros.

Proposition 3.2.2. If the singular values in the singular value decomposition (2) of satisfy the inequalities

then

1. 
2. 
3. 
4. 
5. rank(A)=r;
6. the singular values of A are equal to the semi-axes of the hyperellipsoid
   ;
7. 

Prove the first of these properties. Consider the relation . Since

then

or

Thus,

Proposition 3.2.3. If and is a singular value decomposition of the matrix A, then the column-vectors of are the normed eigenvectors of AA^T and the column-vectors of are the normed eigenvectors of A^TA. Singular values of the matrix A can be found as square roots of the eigenvalues A^TA or AA^T.

Proof. Proceeding from the singular value decomposition of the matrix A we will find expressions of AA^T and A^TA:

 
and
 
Since the matrices and are diagonal matrices, the orthogonal matrices U and V in the expressions (7) and (8) must be formed by the eigenvectors of the matrices AA^T and A^TA respectively.