Definition 2.2.1. A matrix which elements different from zero are only on the main and some adjacent diagonals is called a band matrix.
Definition 2.2.2. It is
said that the matrix ![]() is a band matrix with the lower bandwidth p if
is a band matrix with the lower bandwidth p if
![]()
and with the upper bandwidth q if
![]()
and with the bandwidth p+q+1.
Example 2.2.1. The matrix
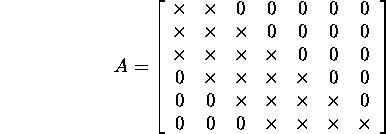
is a band matrix because all the elements different
from zero are on the main and two lower and one upper diagonals. The lower
bandwidth of the matrix A is 2 because aik=0
as i>k+2, and the upper bandwidth
is 1 because aik=0 as k>i+1. The bandwidth
of the matrix is 2+1+1=4. The elements of the matrix that are necessarily
not zeros are denoted by crosses.
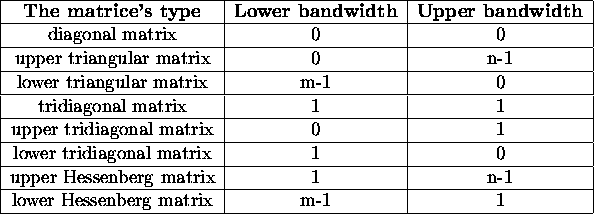
Some most important types of band
matrices are presented in table 2.2.1. If ![]() is a diagonal matrix,
is a diagonal matrix, ![]() and
and ![]() then the notation
then the notation ![]() will be used.
will be used.
Table 2.2.1.
Problem 2.2.1.* Find the type, lower
bandwidth, upper bandwidth and bandwidth
of the matrix A if
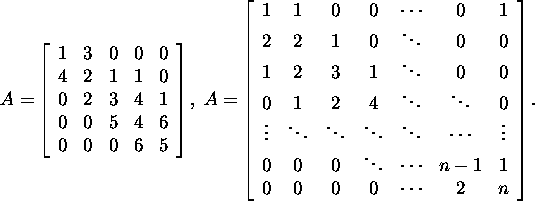
Definition 2.2.3. A matrix
![]() is called a
is called a ![]() block
matrix if
block
matrix if
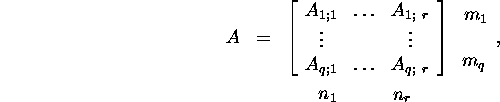
where ![]() and
and ![]() and
and ![]() is a
is a ![]() matrix.
matrix.
Example 2.2.2. The matrix
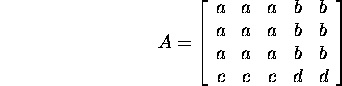
is a ![]() block
matrix, where
block
matrix, where ![]() and n2=2 and
and n2=2 and
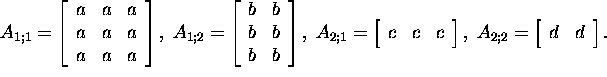
Let
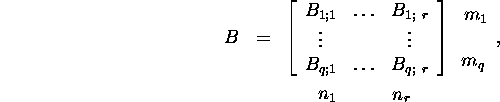
and C=A+B. Then
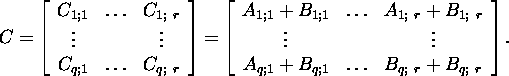
Proposition 2.2.1.
If ![]() and C=AB are block matrices:
and C=AB are block matrices:
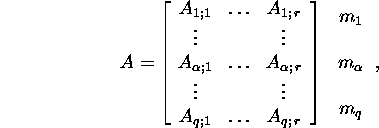
![]()
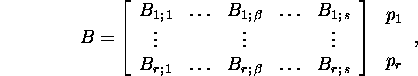
![]()
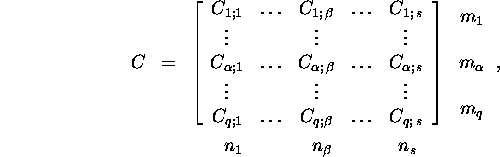
where ![]()
![]()
![]() , then
, then
![]()
Proof. Let
![]()
![]()
As ![]() is an element of the block
is an element of the block ![]() of the matrix C standing in the i-th row and k-th
column of this block, and
of the matrix C standing in the i-th row and k-th
column of this block, and ![]() is an element of the block
is an element of the block ![]() of the matrix A standing in the i-th row and j-th
column of this block, and
of the matrix A standing in the i-th row and j-th
column of this block, and ![]() is an element of the block
is an element of the block ![]() of the matrix B standing in the j-th row and k-th
column, then
of the matrix B standing in the j-th row and k-th
column, then
![]()
Therefore,
![]()
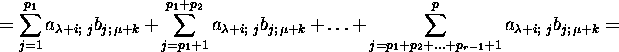
![]()
![]()
Therefore, all the corresponding elements of the matrices ![]() and
and ![]() are equal, and our proposition holds.
are equal, and our proposition holds. ![]()
Corollary 2.2.1. If
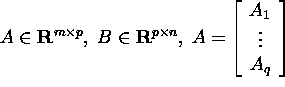
![]()
![]()
![]()
and ![]() and
and ![]() then
then
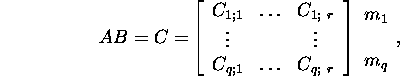
![]()
where ![]() =
1 : q
=
1 : q![]() =
1 : r) .
=
1 : r) .
Example 2.2.3. It holds
![]()
Example 2.2.4. It holds
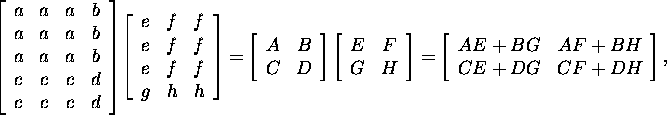
where A=(a) is a ![]() matrix,
B=(b) is a
matrix,
B=(b) is a ![]() matrix,
C=(c) is a
matrix,
C=(c) is a ![]() matrix,
D=(d) is a
matrix,
D=(d) is a ![]() matrix,
E=(e) is a
matrix,
E=(e) is a ![]() matrix,
F=(f) is a
matrix,
F=(f) is a ![]() matrix,
G=(g) is a
matrix,
G=(g) is a ![]() matrix
and H=(h) is a
matrix
and H=(h) is a ![]() matrix.
matrix.
Example 2.2.5.* Let us find the product
AB of block matrices A and B, when A and B
are ![]() matrices
matrices
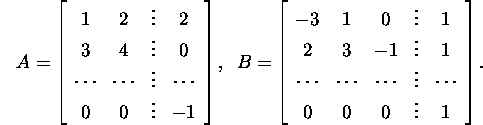
We denote
![]()
where
![]()
and
![]()
We note that the dimensions of the matrices are in accordance with the
conditions of multiplication of block matrices.
If we denote
![]()
then
![]()
![]()
![]()
and
![]()
Thus
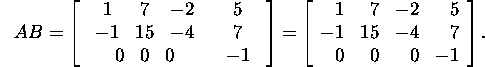
Problem 2.2.2.* Find the product AB
of ![]() -matrix
A and
-matrix
A and ![]() matrix
B in block form, when
matrix
B in block form, when
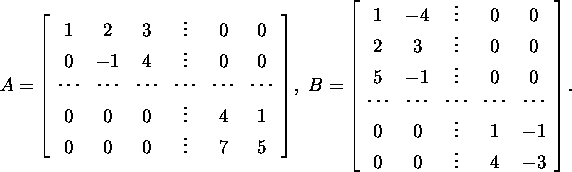
![]()
![]()
![]()