Multiplying (73) by an arbitrary weight function v(x) and integrating over the interval [a,b] one obtains

Evidently (73) and (75) are equivalent, because v(x) is an arbitrary function. Now we seek a numerical solution to (75), (74) in the form

Here , ..., are functions of x and a₁, ..., a_n are unknown coefficients.

In vector form (76) becomes

where

In (75) we may substitute u by u^* to obtain

However, substituting u(x) by its approximation u^*(x) in (73), generally it appears that (73) is not satisfied exactly, e.g.

Here e(x) is a measure for the error.

It follows from (79)-(80) that

Obviously, the residual, e(x), depends on the unknown parameters given by vector . Therefore the coefficients a₁, ..., a_n must be determined so, that expression (81) is satisfied.

Generally

where V₁, ..., V_n are known functions of x and c₁, .., c_n are certain parameters. In terms of vector notation (82) reads

where

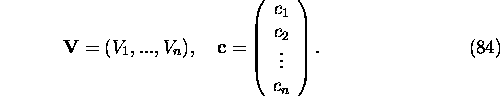
Evidently

and therefore (see (81))

Relation (86) holds for arbitrary c^T- matrices, i.e.

or

Now, we have n equations (88) to determine coefficients a₁,...,a_n. Inserting (77) in (80) yields

and the condition (86) can be rewritten as

Introducing the matrix K and the vector as

we can write (90) in compact form

Finally, we have n linear equations (92) for determing n coefficients a₁,...,a_n.

 
• Point collocation method
• Subdomain collocation method
• Least square method
• Galerkin's method