In the least square method the functions V_i[x] in (82) are defined as

and due to (88) we have

Our interest is the square of the error over interval [a,b]

Next we compute the derivatives

It implies from (101), (103) that

Therefore J is stationary and the square of the error e(x) attains its minimum. In explicit form the linear system (92) reads

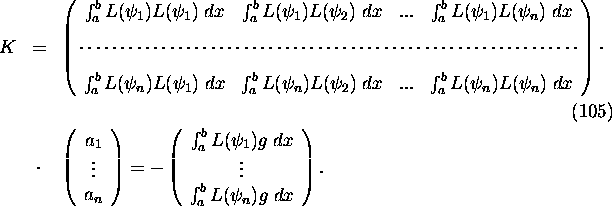
Evidently, the matrix K is symmetric.