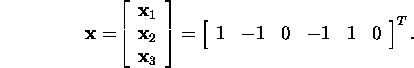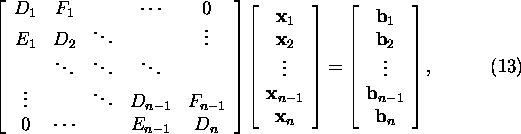
kus
siis
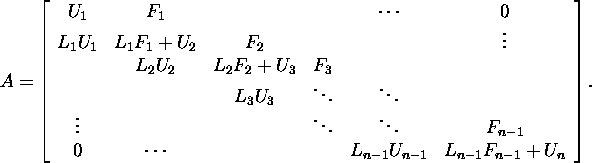
Leiame samm-sammult blokid
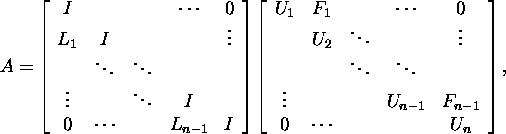
Süsteemi (13) lahendamiseks tuleb kõigepealt lahendada süsteem
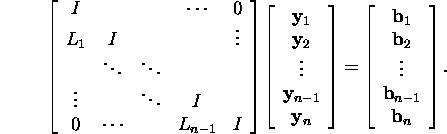
Leiame, et
Teiseks, tuleb lahendada süsteem
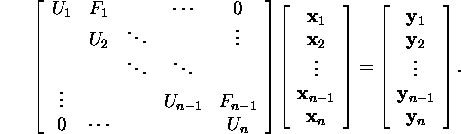
Peatüki
algus: Lineaarsete
algebraliste võrrandisüsteemide lahendamise
Eelmine: Lintmaatriksitega
süsteemid
Järgmine: Võrrandisüsteemide
lahendam ine QR-meetodil
Vaatleme süsteemi kujul
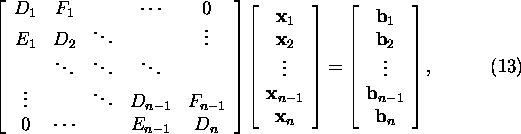
kus ![]() ,
,
![]()
![]() ja
ja ![]() ,
,
![]() Kui esitame maatriksi A kujul
Kui esitame maatriksi A kujul

siis
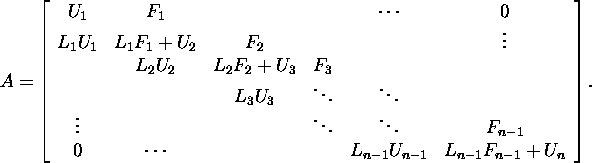
Leiame samm-sammult blokid ![]() ja Ui:
ja Ui:
![]()
![]()
![]()
![]()
Süsteemi (13) lahendamiseks tuleb kõigepealt
lahendada süsteem
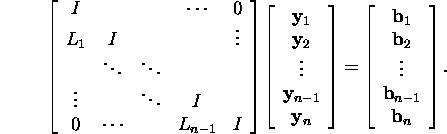
Leiame, et
![]()
![]()
![]()
Teiseks, tuleb lahendada süsteem
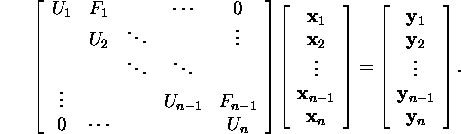
Näide 6.6.1.* Lahendame
võrrandisüsteemi ![]() kus
kus
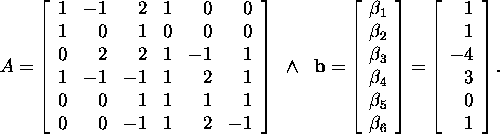
See on seosega (13) esitatud tüüpi blokk-süsteem,
sest
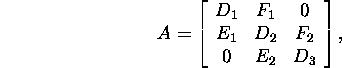
kus ![]() ja
ja
![]()
![]()
Esitame maatriksi A kujul
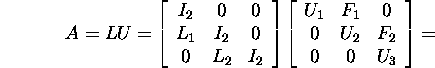
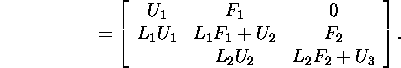
Leiame, et
![]()
![]()
![]()
![]()
![]()
ja
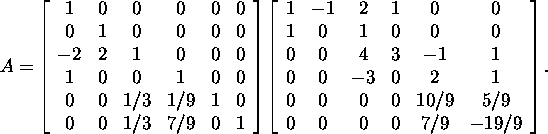
Süsteemi ![]() lahendi leidmiseks lahendame kaks süsteemi
lahendi leidmiseks lahendame kaks süsteemi ![]() ja
ja ![]() Süsteem
Süsteem ![]() on esitatav kujul
on esitatav kujul
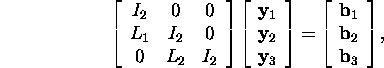
kus
![]()
![]()
ja
![]()
![]()
Süsteemi ![]() mis on esitatav kujul
mis on esitatav kujul
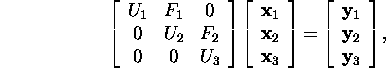
lahendamisel saame, et
![]()
![]()
Seega