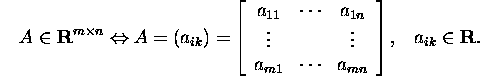
Maatriksi A elementi, mis paikneb i-ndas reas ja k-ndas veerus, tähistatakse aik või A(i,k) või [A]ik. Põhilised operatsioonid maatriksitega on järgmised:
Peatüki
algus: Maatriksid
Eelmine: Maatriksid
Järgmine: Lintmaatriksid
ja blokkmaatriksid
Kõigi reaalsete elementidega ![]() maatriksite
vektorruumi tähistatakse
maatriksite
vektorruumi tähistatakse
![]() ja
ja
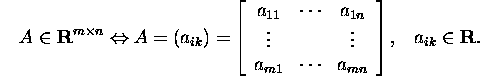
Maatriksi A elementi, mis paikneb i-ndas reas ja k-ndas
veerus, tähistatakse aik või A(i,k)
või [A]ik. Põhilised operatsioonid
maatriksitega on järgmised:
Ülesanne 2.1.1.* Olgu
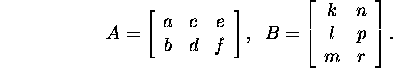
Leidke maatriks AB.
Ülesanne 2.1.2.* Olgu

Leidke maatriks An-1.
Ülesanne 2.1.3.* Olgu
![]()
Tõestage, et
![]()
Näide 2.1.1.* Näitame, et maatriksite
korrutamine ei ole kommutatiivne.
Olgu
![]()
Leiame korrutised:
![]()
![]()
Kuna antud näite korral ![]() siis üldjuhul maatriksite korrutamine ei ole kommutatiivne.
siis üldjuhul maatriksite korrutamine ei ole kommutatiivne.
Lause 2.1.1. Kui ![]() ja
ja ![]() siis
siis
![]()
Tõestus. Kui C=(AB)T,
siis
![]()
Teisalt, kui D=BTAT, siis
![]()
![]()
Definitsioon 2.1.1. Maatriksit
![]() nimetatakse sümmeetriliseks maatriksiks, kui AT=A
ja kaldsümmeetriliseks maatriksiks, kui AT
=-A.
nimetatakse sümmeetriliseks maatriksiks, kui AT=A
ja kaldsümmeetriliseks maatriksiks, kui AT
=-A.
Ülesanne 2.1.4.* Kas maatriks A
on sümmeetriline maatriks või
kaldsümmeetriline maatriks, kui
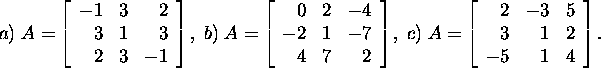
Lause 2.1.2. Suvaline maatriks ![]() on esitatav sümmeetrilise maatriksi ja
kaldsümmeetrilise maatriksi summana.
on esitatav sümmeetrilise maatriksi ja
kaldsümmeetrilise maatriksi summana.
Tõestus. Suvaline maatriks ![]() on esitatav kujul A=B+C, kus B=(A+AT)/2
ja C=(A-AT)/2. Kuna
on esitatav kujul A=B+C, kus B=(A+AT)/2
ja C=(A-AT)/2. Kuna
![]()
ja
![]()
siis lause väide peab paika.
Ülesanne 2.1.5.* Esitage maatriks
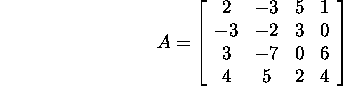
sümmeetrilise maatriksi ja kaldsümmeetrilise
maatriksi summana.
Definitsioon 2.1.2.
Kui A on kompleksarvuliste elementidega ![]() maatriks,
st
maatriks,
st ![]() siis maatriksi A transponeeritud kaasmaatriks AH
defineeritakse seosega
siis maatriksi A transponeeritud kaasmaatriks AH
defineeritakse seosega
![]()
Definitsioon 2.1.3. Maatriksit
![]() nimetatakse Hermite'i maatriksiks, kui
nimetatakse Hermite'i maatriksiks, kui
![]()
Ülesanne 2.1.6.* Kas maatriks A
on Hermite'i maatriks, kui
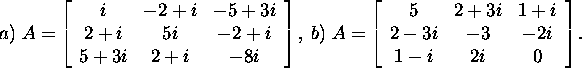
Ülesanne 2.1.7. * Olgu ![]() Näidake, et maatriksid AAH ja AHA
on Hermite'i maatriksid.
Näidake, et maatriksid AAH ja AHA
on Hermite'i maatriksid.
Maatriksit ![]() on võimalik esitada nii maatriksi A veeruvektorite
on võimalik esitada nii maatriksi A veeruvektorite ![]() abil kui ka maatriksi A transponeeritud reavektorite
abil kui ka maatriksi A transponeeritud reavektorite ![]() )
abil (''kleepides'' maatriksi kokku vastavalt veeruvektoreist või
transponeeritud reavektoreist)
)
abil (''kleepides'' maatriksi kokku vastavalt veeruvektoreist või
transponeeritud reavektoreist)
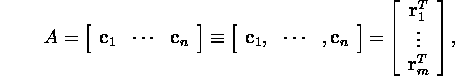
kusjuures ![]() ja
ja ![]() ning
ning
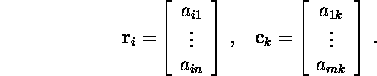
Näide 2.1.1. Illustreerime neid mõisteid
järgmise maatriksi ![]() abil
abil
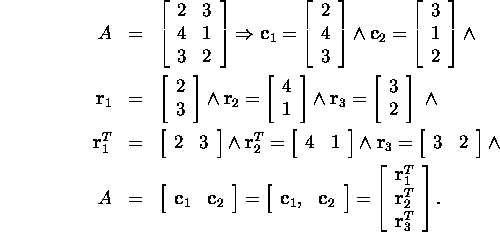
Kui ![]() siis A(i,:) tähistab maatriksi A
siis A(i,:) tähistab maatriksi A ![]() -ndat
rida, st
-ndat
rida, st
![]()
ja ![]() k-ndat veergu, st
k-ndat veergu, st
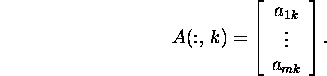
Kui ![]() siis
siis
![]()
ja kui ![]() siis
siis
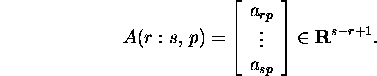
Kui ![]() ja
ja ![]() ning
ning ![]() kusjuures
kusjuures
![]()
siis vastav osamaatriks on
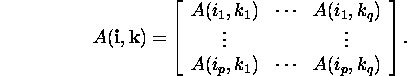
Näide 2.1.2. Kui
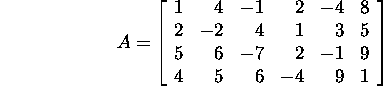
ja ![]() ja
ja ![]() siis
siis
![]()