ja ülemise ribalaiusega q, kui
ning lindilaiusega p+q+1.
Peatüki
algus: Maatriksid
Eelmine: Maatriksi
tähistus ja tehted
Järgmine: Determinandid
Definitsioon 2.2.1. Maatriksit, mille nullist erinevad elemendid on ainult peadiagonaalil ja selle mõningatel naaberdiagonaalidel, nimetatakse lintmaatriksiks.
Definitsioon 2.2.2. Öeldakse,
et maatriks ![]() on lintmaatriks lindi alumise ribalaiusega p, kui
on lintmaatriks lindi alumise ribalaiusega p, kui
![]()
ja ülemise ribalaiusega q, kui
![]()
ning lindilaiusega p+q+1.
Näide 2.2.1. Maatriks
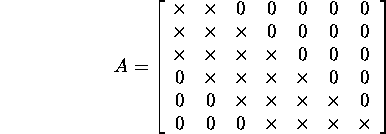
on lintmaatriks, sest selle nullist erinevad
elemendid asetsevad peadiagonaalil ja selle kahel alumisel naaberdiagonaalil
ning ühel ülemisel naaberdiagonaalil. Maatriksi A alumine
ribalaius on 2, sest aik=0, kui i>k+2,
ja ülemine ribalaius on 1, sest aik=0,
kui k>i+1. Maatriksi lindi laius on 2+1+1=4. Maatriksi
elemendid, mis ei pruugi olla nullid, on siin tähistatud ristikestega.
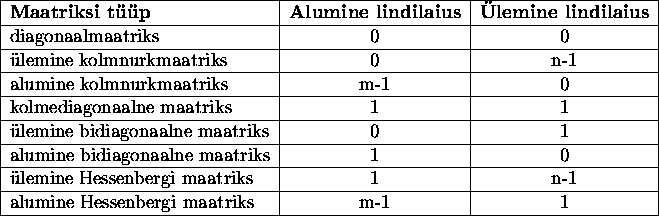
Mõned olulisemad lintmaatriksite tüübid
esitame tabeli 2.2.1 kujul. Kui ![]() on diagonaalmaatriks,
on diagonaalmaatriks, ![]() ja
ja ![]() siis kasutatakse tähistust
siis kasutatakse tähistust ![]()
Ülesanne 2.2.1.* Leidke maatriksi
A tüüp, alumine
ribalaius, ülemine ribalaius ja maatriksi
lindilaius, kui
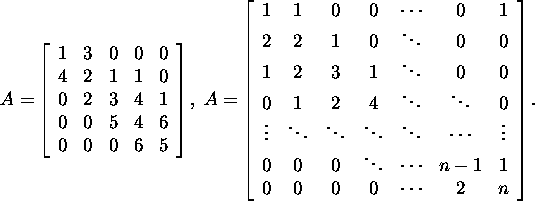
Definitsioon 2.2.3. Maatriksit
![]() nimetatakse
nimetatakse ![]() -blokkmaatriksiks,
kui
-blokkmaatriksiks,
kui
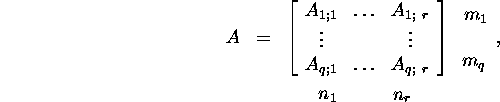
kus ![]() ja
ja ![]() ning
ning ![]() on
on ![]() maatriks.
maatriks.
Näide 2.2.2. Maatriks
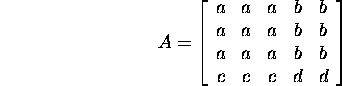
on ![]() blokkmaatriks,
kusjuures
blokkmaatriks,
kusjuures ![]() ja n2=2 ning
ja n2=2 ning
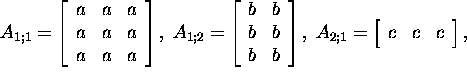
![]()
Olgu
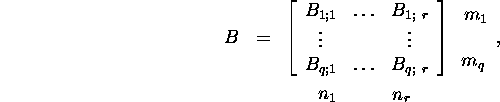
ja C=A+B, siis
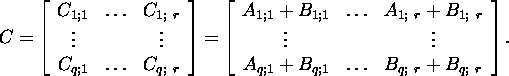
Lause 2.2.1. Kui ![]() on blokkmaatriksid,
on blokkmaatriksid,
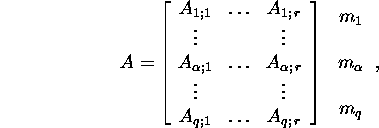
![]()
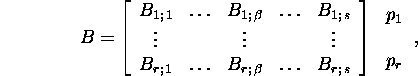
![]()
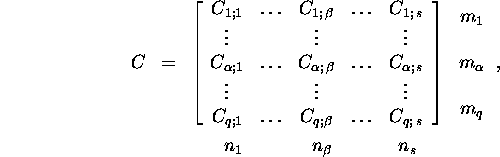
kusjuures ![]()
![]()
![]() , siis
, siis
![]()
Tõestus. Olgu
![]()
![]()
Kuna ![]() on maatriksi C bloki
on maatriksi C bloki ![]() element, mis paikneb selle bloki i-ndas reas ja k-ndas veerus,
ja
element, mis paikneb selle bloki i-ndas reas ja k-ndas veerus,
ja ![]() maatriksiA bloki
maatriksiA bloki ![]() element, mis paikneb selle bloki i-ndas reas ja j-ndas veerus,
ning
element, mis paikneb selle bloki i-ndas reas ja j-ndas veerus,
ning ![]() maatr iksi B bloki
maatr iksi B bloki ![]() element, mis paikneb selle bloki j-ndas reas ja k-ndas veerus,
siis
element, mis paikneb selle bloki j-ndas reas ja k-ndas veerus,
siis
![]()
Seega,
![]()
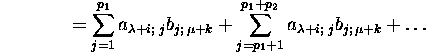
![]()
![]()
![]()
Järelikult, maatriksite ![]() ja
ja ![]() kõik vastavad elemendid on võrdsed ja seega lause väide
peab paika.
kõik vastavad elemendid on võrdsed ja seega lause väide
peab paika.
Järeldus 2.2.1. Kui 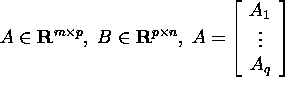
![]()
![]()
![]()
ja ![]() ning
ning ![]() siis
siis
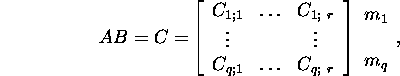
![]()
kus ![]() =
1:q
=
1:q![]() =1
:r).
=1
:r).
Järeldus 2.2.2. Kui ![]()
![]()
![]()
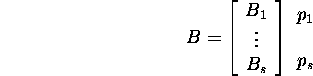
ja ![]()
![]() siis
siis
![]()
Näide 2.2.3. Kehtib võrdus
![]()
Näide 2.2.4. Kehtib võrdus
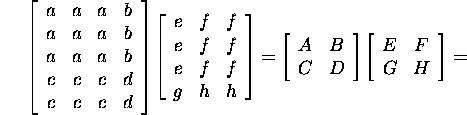
![]()
kus A=(a) on ![]() -maatriks,
B=(b) on
-maatriks,
B=(b) on ![]() -maatriks,
C=(c) on
-maatriks,
C=(c) on ![]() -maatriks,
D=(d) on
-maatriks,
D=(d) on ![]() -maatriks,
E=(e) on
-maatriks,
E=(e) on ![]() -maatriks,
F=(f) on
-maatriks,
F=(f) on ![]() -maatriks,
G=(g) on
-maatriks,
G=(g) on  -maatriks
ja H=(h) on
-maatriks
ja H=(h) on ![]() -maatriks.
-maatriks.
Näide 2.2.5.* Leiame blokkmaatriksite
A ja B korrutise AB, kui A ja B on ![]() maatriksid,
kusjuures
maatriksid,
kusjuures
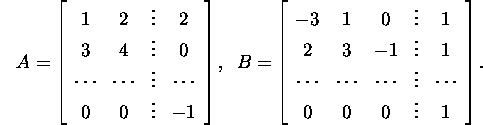
Tähistame
![]()
kusjuures
![]()
ja
![]()
Nendime, et on täidetud mõõdete kooskõla tingimused
blokkmaatriksite korrutamiseks. Kui tähistada
![]()
siis
![]()
![]()
![]()
ja
![]()
Seega
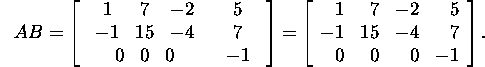
Ülesanne 2.2.2.* Leidke ![]() -maatriksi
A ja
-maatriksi
A ja ![]() maatriksi B korrutis AB
blokkkujul, kui
maatriksi B korrutis AB
blokkkujul, kui
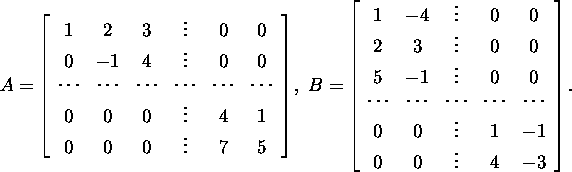
Peatüki
algus: Maatriksid
Eelmine: Maatriksi
tähistus ja tehted
Järgmine: Determinandid