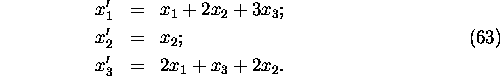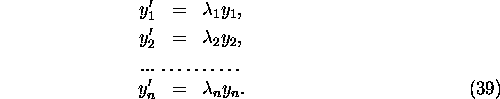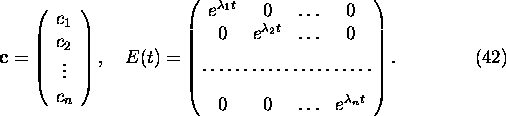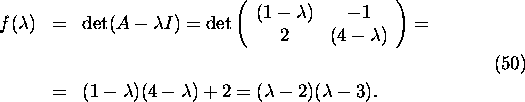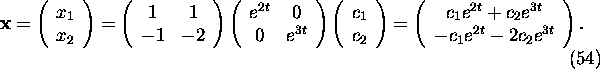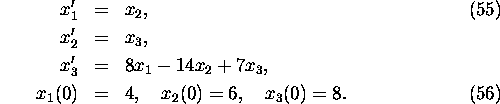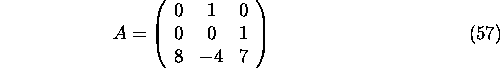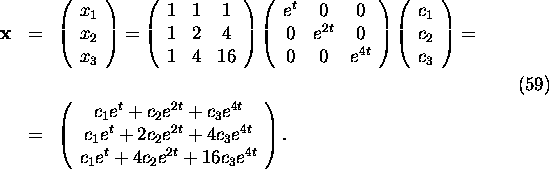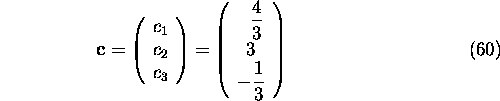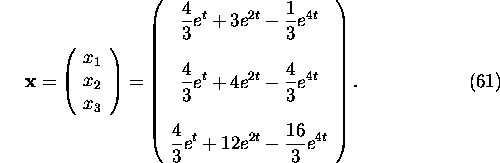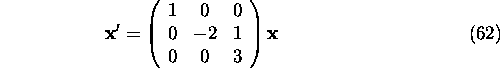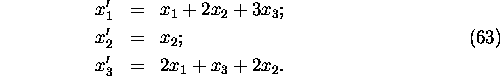We assume, that nxn matrix A is diagonalisable over 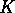, i.e. it has n linearily independent eigenvectors 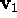, ..., 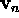belonging to eigenvalues 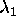, ..., 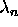over 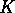(here or )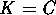

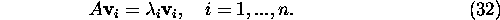
Assembling the eigenvectors into nxn matrix S

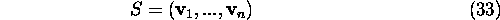
we can write

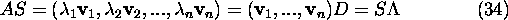
where 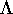is a nxn diagonal matrix with entries 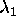, ..., 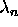. Multiplying (34) on the right by S^-1 one obtains the matrix A in diagonally factorised form

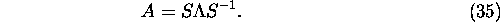
Substituting (35) in (2) and multiplying obtained result on the left by S^-1 yields

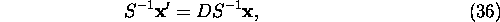
or

Here a vector 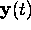is defined as

Evidently, the system of differential equations (37) is a diagonal system, because the matrix D is diagonal. In explicit form the system (37) reads

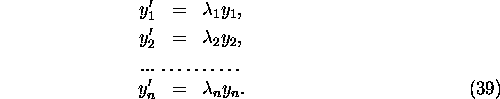
Integrating (39), we obtain

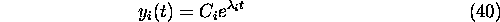
or in matrix form

where

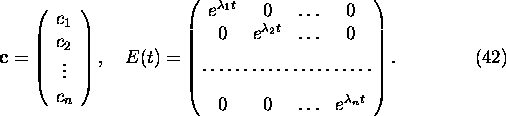
Substituting (38) in (41) and multiplying obtained result on the left by S one obtains the general solution of system (2) in terms of original variables x

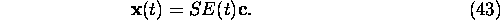
The vector of integration constants can be determined satisfying the initial conditions 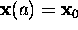(or boundary conditions (4)).

Satisfaction condition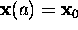s gives

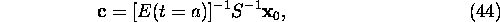
and

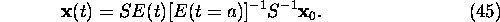
In most practical case (a=0), the formula (45) reduces to

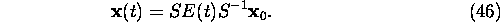
General solution algorithm using linear algebra software is following:

1. find the eigenvalues and eigenvectors

2. compose matrices S and E(t)

3. compute the general solution to (1) by (43) or solution to the initial value problem by (46).

Example 1: Consider the system

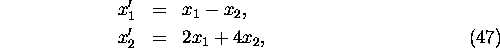
find the general solution.

In matrix notation the system (47) becomes

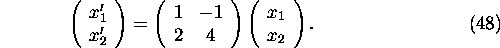
The characteristic polynomial of matrix A

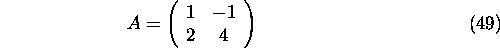
is

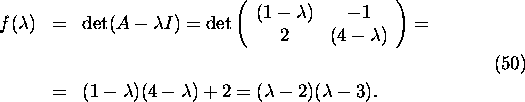
Therefore the eigenvalues are 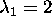and 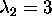. The eigenvector 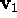associated with 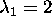is obtained by solving equation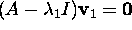

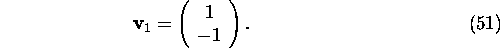
Analogically

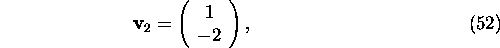
and therefore

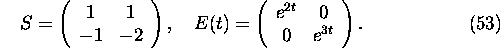
Finally, we can compute the general solution of system (47) using formula (53)

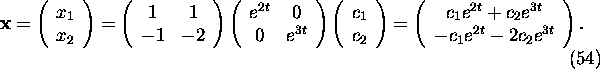
Example 2: Solve the following initial value problem

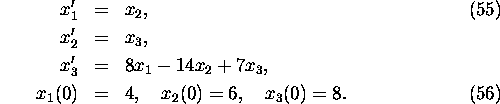
For the system (55) the matrix

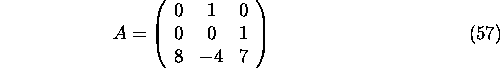
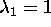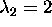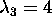has eigenvalues , and . Associated eigenvectors are

respectively.

The general solution of system (55) is given by

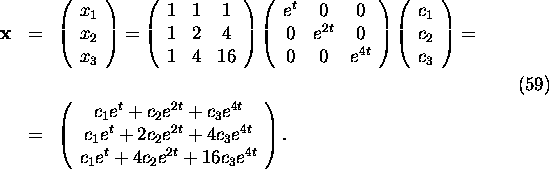
From (44) the integration constants are

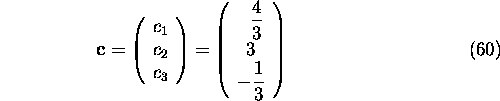
and the solution of the initial value problem (45)-(46) can be presented as

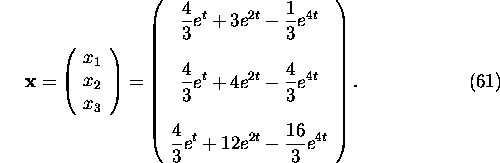
Exercises
1. Consider a linear system of differential equations

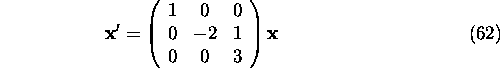
a) find the general solution
b) find the solution to the initial value problem determined by the initial conditions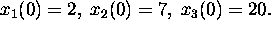

2. Find the general solution to the linear system of differential equations.