where
Using the scalar equation as a quide, we assume that the vector
equation (2) has a solution of the form
![]()
where ![]() is a constant vector.
is a constant vector.
Substituting the solution (5) in left and right side of equation
(2) yields
![]()
![]()
Evidently, the vector equation (2) is satisfied only, if
![]()
i.e.
![]()
Therefore, if ![]() is an eigenvalue of A and
is an eigenvalue of A and ![]() is a
corresponding eigenvector, then
is a
corresponding eigenvector, then ![]() is a solution to
is a solution to ![]() (
(![]() gives a trivial solution). Obviously, the solutions
gives a trivial solution). Obviously, the solutions
![]()
associated with eigenvalues ![]() , ...,
, ..., ![]() and
eigenvectors
and
eigenvectors ![]() , ...,
, ..., ![]() , are linearily
independent. It is easy to verify that any linear combination of
, are linearily
independent. It is easy to verify that any linear combination of
![]() , ...,
, ..., ![]() is also a solution. The
general solution to the vector equation (2) is given by
is also a solution. The
general solution to the vector equation (2) is given by
![]()
Substituting (10) in (11) yields
![]()
The initial value problem consists in finding a solution to (2) that
satisfies an initial condition
![]()
It follows from (12), (13) that
![]()
Determining the integration constants from linear algebraic system
(14) and inserting in (12) one obtains the solution to initial
value problem (1), (13).
General solution algorithm using linear algebra software (MATLAB, MAPLE,...) is following:
1. find the eigenvalues and eigenvectors
2. compose the general solution
3. determine the integration constants
4. compose the solution to the initial value problem.
Note: Steps 3-4 must be filled only for initial value problems.
Example 1: Solve the initial value problem
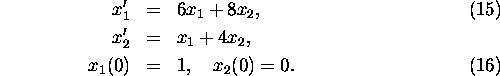
In matrix notation the system (15) reads
![]()
The characteristic polynomial of the matrix A is
![]()
Hence, the eigenvalues are ![]() and
and ![]() .
Substituting the eigenvalues
.
Substituting the eigenvalues ![]() and
and ![]() in
(9), we can determine corresponding eigenvectors
in
(9), we can determine corresponding eigenvectors
![]()
Now, the general solution of equation (15) can be presented as
![]()
The initial conditions (16) in matrix notation take the form
![]()
It follows from (20), (21) that
![]()
Solving system (22) yields: ![]() and
and ![]() . Inserting
. Inserting ![]() and
and ![]() into general
solution (20) gives the solution to the initial value problem (15),
(16) as
into general
solution (20) gives the solution to the initial value problem (15),
(16) as
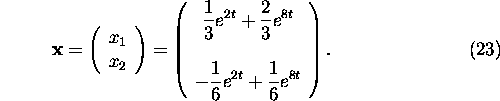
Example 2: Find the general solution to the linear system of
differential equations
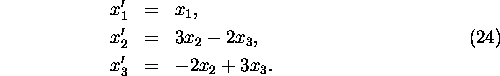
The matrix of system (24)
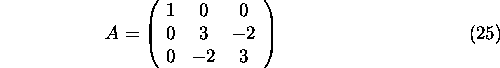
has the eigenvalues ![]() and
and ![]() .
So,
.
So, ![]() is an eigenvalue of multiplicity 2. Generally, if
is an eigenvalue of multiplicity 2. Generally, if
![]() is an eigenvalue of A of multiplicity k, and the
rank of the matrix
is an eigenvalue of A of multiplicity k, and the
rank of the matrix ![]() is equal to n-k, then we can
find k linearily independent eigenvectors of A associated with
the eigenvalue
is equal to n-k, then we can
find k linearily independent eigenvectors of A associated with
the eigenvalue ![]() . For given A with (25)
. For given A with (25)
![]()
Therefore, we can find two linearily independent eigenvectors
associated with ![]() using relation (9)
using relation (9)
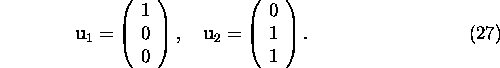
Computing the eigenvector ![]() associated with the
eigenvalue
associated with the
eigenvalue ![]()
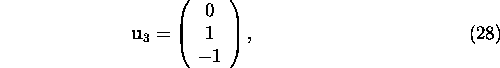
we can determine the general solution to system (24) as
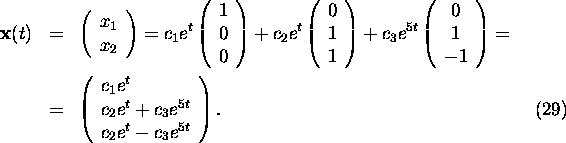
Exercises
1. Solve the initial value problem
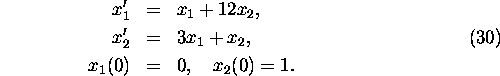
2. Find the general solution of the following linear system of
differential equations:
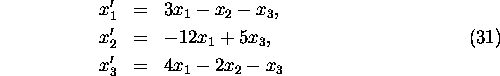
3. Solve two point boundary value problem with differential equations (30) and boundary conditions x1(1)=1 and x2(0)=0.