Peatüki algus: LU-lahutus
Eelmine: LU-lahutus
Järgmine: Gaussi teisendus ja L U-lahutus

Vaatleme alumise -kolmnurkmaatriksiga võrrandisüsteemi

lahendamist asendusega edasisuunas. Esimesest võrrandist saame ja siis teisest võrrandist

Lause 1.1.1 (asendused edasisuunas). Kui on alumine kolmnurkmaatriks ja ning siis lahend on

Lahendame ülemise kolmnurkmaatriksiga võrrandisüsteemi

asendusega tagasisuunas. Teisest võrrandist saame ja siis esimesest võrrandist

Lause 1.1.2 (asendused tagasisuunas). Kui on ülemine kolmnurkmaatriks ja ning siis lahend on

Nii edasi kui tagasi suunatud asenduse korral tuleb regulaarse kolmnurkmaatriksiga süsteemi lahendamisel sooritada tehet.

Lause 1.1.3 (veeru elimineerimine asendustel edasisuunas). Kui on alumine kolmnurkmaatriks, ja ning on leitud, siis asendades suuruse võrrandeisse teisest kuni n-ndani, saame uue alumise kolmnurkmaatriksiga süsteemi

Lause 1.1.4 (veeru elimineerimine asendustel tagasisuunas). Kui on ülemine kolmnurkmaatriks, ja ning on leitud, siis asendades võrrandeisse esimesest kuni (n-1)-seni, saame uue ülemise kolmnurkmaatriksiga süsteemi

Vaatleme veel mitme süsteemi samaaegset lahendamist juhul, kui neil süsteemidel on ühine süsteemimaatriks. Vaatleme süsteemi LX=B, kus on regulaarne alumine kolmnurkmaatriks ja ning otsitavaks on . Esitame selle süsteemi blokk-kujul
 
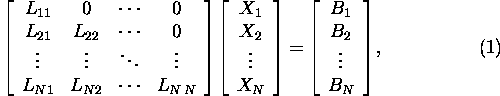
kusjuures digonaalil on ruutblokid. Võrrandist saame leida maatriksi X₁. Kasutades lauses 1.1.3 antud veeru elimineerimise võtet süsteemi (1) korral, saame

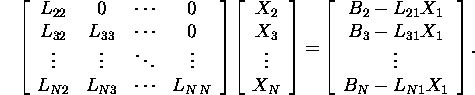
Nii, samm-sammult, lahendame süsteemi (1).

Lause 1.1.5. Kolmnurkmaatriksitel on järgmised omadused:

• ülemise (alumise) kolmnurkmaatriksi pöördmaatriks on ülemine (alumine) kolmnurkmaatriks;
• kahe ülemise (alumise) kolmnurkmaatriksi korrutis on ülemine (alumine) kolmnurkmaatriks;
• ülemise (alumise) kolmnurkmaatriksi, mille determinant on üks, pöördmaatriks on ülemine (alumine) kolmnurkmaatriks determinandiga üks;
• kahe ülemise (alumise) kolmnurkmaatriksi, mille determinant on üks, korrutis on ülemine (alumine) kolmnurkmaatriks determinandiga üks.

Ülesanne 1.1.1.^* Tõestage lause 1.1.5.