


Next: The deconfinement phase transition
Up: Calculation
Previous: The fermionic bag constant
How do confined gluons alter the results obtained so far?
Analogous to the fermionic case the gluonic bag constant 8 x Bg is defined
as the vacuum expectation value of the following quadratic
boundary condition [6]
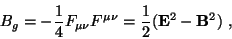 |
(5) |
where to lowest order in the coupling the
field strength tensor 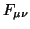 is Abelian, and
is Abelian, and 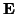 and
and 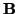 denote the electric and
magnetic field strength, respectively. Appealing in the sourceless case
to the symmetry of Maxwell's equations under the
duality transformation
denote the electric and
magnetic field strength, respectively. Appealing in the sourceless case
to the symmetry of Maxwell's equations under the
duality transformation
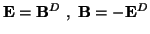 ,
we obtain due to physical transverse polarizations (TE,TM)
the following expression for Bg in Feynman gauge
,
we obtain due to physical transverse polarizations (TE,TM)
the following expression for Bg in Feynman gauge
Thereby, the superscript D indicates that the corresponding
eigenvalue has been obtained from the linear boundary
condition
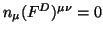 for the dual field strength, and
for the dual field strength, and
 (
(
 )
denotes the normalization
constant for the corresponding mode.
For technicalities concerning Cavity QCD in
Feynman gauge see Refs. [26,27].
In Eq.(6), the introduction of the Schwinger parameter z
and the subsequent truncation of the z-integration and
mode summation due to the subtraction of hard
fluctuations in the vacuum is analogous to the fermionic case.
Table 3 contains the values for 8 x Bg under
variations of R with
)
denotes the normalization
constant for the corresponding mode.
For technicalities concerning Cavity QCD in
Feynman gauge see Refs. [26,27].
In Eq.(6), the introduction of the Schwinger parameter z
and the subsequent truncation of the z-integration and
mode summation due to the subtraction of hard
fluctuations in the vacuum is analogous to the fermionic case.
Table 3 contains the values for 8 x Bg under
variations of R with 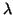 adjusted to
adjusted to  GeV and
GeV and 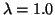 GeV.
For radii R less than R=0.7 fm there is no contribution from
the mode sum of Eq.(6).
GeV.
For radii R less than R=0.7 fm there is no contribution from
the mode sum of Eq.(6).
Table:
The dependence of the gluonic bag constant
on the cutoff
 with R ranging from 0.4 fm to 1.0 fm.
The lower and upper values of
with R ranging from 0.4 fm to 1.0 fm.
The lower and upper values of 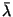 correspond to
correspond to
 and
and 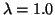 GeV, respectively.
GeV, respectively.
|
R [fm] |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
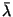
|
1.6 |
1.8 |
2.0 |
2.25 |
2.4 |
2.7 |
2.8 |
3.15 |
3.2 |
3.6 |
3.6 |
4.05 |
4.0 |
4.5 |
|
8 x Bg [GeV4] |
0 |
0 |
0 |
0 |
0 |
0 |
0.0133 |
0.0205 |
0.0128 |
0.0189 |
0.0179 |
0.0302 |
0.0191 |
0.0271 |
We find stability for 8 x Bg
under a variation of R at R=0.8 fm with
8 x Bg=0.0128 GeV4 for  GeV and with
8 x Bg=0.0189 GeV4 for
GeV and with
8 x Bg=0.0189 GeV4 for 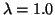 GeV.
Appealing to the QCD trace anomaly and requiring that the total bag constant
GeV.
Appealing to the QCD trace anomaly and requiring that the total bag constant
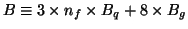 produces the
central value of the gluon condensate, implies
produces the
central value of the gluon condensate, implies 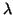 to be less than
to be less than  GeV.
As far as the properties of the lowest
light-flavor resonances are concerned, which are believed to be strongly correlated with the QCD
condensates of lowest mass-dimension, QCD sum rules [28]
suggest the onset of the perturbative
regime at values of about 1.5-1.8 GeV2 of the
spectral continuum threshold s0 [23,29,30,31].
This corresponds to
GeV.
As far as the properties of the lowest
light-flavor resonances are concerned, which are believed to be strongly correlated with the QCD
condensates of lowest mass-dimension, QCD sum rules [28]
suggest the onset of the perturbative
regime at values of about 1.5-1.8 GeV2 of the
spectral continuum threshold s0 [23,29,30,31].
This corresponds to 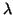 =1.22-1.34 GeV.
Hence, our value of
=1.22-1.34 GeV.
Hence, our value of
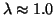 GeV for the pure quark bag
seems already a bit too small which might be due to
the mode sum representation of the
cavity propagator with implicit spatial correlations, whereas
s0 relates to plane-wave states.
Nevertheless, it is hard to accept values of
GeV for the pure quark bag
seems already a bit too small which might be due to
the mode sum representation of the
cavity propagator with implicit spatial correlations, whereas
s0 relates to plane-wave states.
Nevertheless, it is hard to accept values of 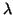 lower than 0.8 GeV for the mixed bag.
lower than 0.8 GeV for the mixed bag.



Next: The deconfinement phase transition
Up: Calculation
Previous: The fermionic bag constant
Marc Schumann
2000-10-16