


Next: The gluonic bag constant
Up: Calculation
Previous: The canonical vacuum energy
Due to the vacuum expectation value of the
quadratic boundary condition, the fermionic bag
constant Bq reads
Figure 1:
The canonical part of the one-flavor, one-color vacuum
energy in dependence on the cutoff. Both quantities are given in units of R-1.
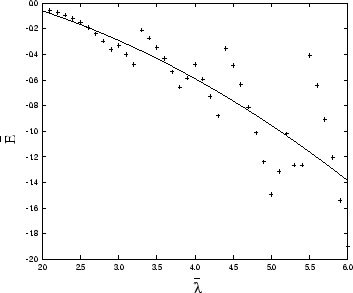 |
Figure 1 shows the result of the calculation of
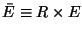 as a function of
as a function of
 .
The
discontinuous behavior is due to the fact that mode
eigenvalues at low energies are not spaced equidistantly.
To smooth the ``nervous'' behavior, we use a quadratic regression as indicated by the solid line.
In Fig. 2 the
.
The
discontinuous behavior is due to the fact that mode
eigenvalues at low energies are not spaced equidistantly.
To smooth the ``nervous'' behavior, we use a quadratic regression as indicated by the solid line.
In Fig. 2 the 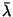 dependence of
dependence of
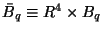 is depicted.
Again, a quadratic fit is used to average over discontinuities.
Tables 1 and 2 contain a list of values for
3 x nf x Bq,
-3 x nf x E under variation of R, where
is depicted.
Again, a quadratic fit is used to average over discontinuities.
Tables 1 and 2 contain a list of values for
3 x nf x Bq,
-3 x nf x E under variation of R, where 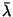 is adjusted to
is adjusted to
 GeV,
GeV,  GeV and
GeV and
 GeV,
GeV, 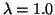 GeV, respectively. Thereby,
nf=2 stands for the light-flavor multiplicity, and the factor three
is the number of colors.
GeV, respectively. Thereby,
nf=2 stands for the light-flavor multiplicity, and the factor three
is the number of colors.
Figure 2:
The one-flavor, one-color fermionic bag constant in dependence on
the cutoff. The bag constant and the cutoff are given
in units of R-4 and R-1, respectively.
 |
Table:
The dependence of the fermionic bag constant and the canonical part of the
fermionic vacuum energy on the cutoff
 for two
light-quark flavors with R ranging from 0.4 fm to 1.0 fm.
The lower and upper values of
for two
light-quark flavors with R ranging from 0.4 fm to 1.0 fm.
The lower and upper values of 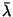 correspond to
correspond to
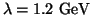 and
and  GeV, respectively.
GeV, respectively.
|
R [fm] |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
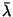
|
2.4 |
3.2 |
3.0 |
4.1 |
3.6 |
4.9 |
4.3 |
5.7 |
4.9 |
6.5 |
5.5 |
7.3 |
6.1 |
8.1 |
|
3 x nf x Bq[GeV4] |
0.032 |
0.053 |
0.024 |
0.079 |
0.021 |
0.089 |
0.026 |
0.088 |
0.028 |
0.082 |
0.028 |
0.075 |
0.027 |
0.068 |
|
-3 x nf x E [GeV] |
0.450 |
1.060 |
0.716 |
1.439 |
0.942 |
1.779 |
1.145 |
2.095 |
1.334 |
2.398 |
1.513 |
2.690 |
1.686 |
2.976 |
Table:
Same as in Table 1.
The lower and upper values of 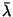 correspond to
correspond to
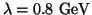 and
and 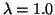 GeV, respectively.
GeV, respectively.
|
R [fm] |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
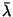
|
1.6 |
2.0 |
2.0 |
2.5 |
2.4 |
3.0 |
2.8 |
3.5 |
3.2 |
4.1 |
3.6 |
4.6 |
4.1 |
5.1 |
|
3 x nf x Bq [GeV4] |
0.129 |
0.065 |
0.027 |
0.011 |
0.006 |
0.007 |
0.003 |
0.010 |
0.003 |
0.012 |
0.004 |
0.013 |
0.005 |
0.014 |
|
-3 x nf x E [GeV] |
-0.031 |
0.193 |
0.154 |
0.415 |
0.300 |
0.597 |
0.422 |
0.755 |
0.530 |
0.900 |
0.628 |
1.034 |
0.720 |
1.162 |
Appealing to the one-loop trace-anomaly [22] of the
QCD energy-momentum tensor

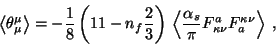 |
(3) |
we assume for the moment that only quark fluctuations
contribute to the bag constant. Using the fact
that the canonical part of
 is traceless in the mixed MIT bag model, we obtain (apart from a sign) the relation
is traceless in the mixed MIT bag model, we obtain (apart from a sign) the relation
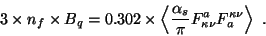 |
(4) |
Thereby, the value of the (renormalization-scale independent)
gluon condensate [23] is
 .
Comparing by means of Eq.(4) the central value of the gluon condensate
with the values of
3 x nf x Bq (Tables 1, 2), which are
stable under variation of R, we obtain agreement
for
.
Comparing by means of Eq.(4) the central value of the gluon condensate
with the values of
3 x nf x Bq (Tables 1, 2), which are
stable under variation of R, we obtain agreement
for 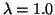 GeV and a bag radius R of 0.6 fm.
Given these values of
GeV and a bag radius R of 0.6 fm.
Given these values of 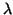 and R, the results of
Table 2 indicate that
-3 x nf x E is
close to phenomenologically obtained values:
In Ref.[9] Z0 parametrizes the
Casimir energy as -Z0/R. Fits to the hadron
spectrum yield values of about Z0=2 [9].
The effect of the center-of-mass contribution to Z0
was found to be of the order of 40% in Refs.[24,25].
In comparison, our value of
-3 x nf x E=0.597 GeV at R=0.6 fm corresponds to
Z0=1.79 with no center-of-mass contribution.
and R, the results of
Table 2 indicate that
-3 x nf x E is
close to phenomenologically obtained values:
In Ref.[9] Z0 parametrizes the
Casimir energy as -Z0/R. Fits to the hadron
spectrum yield values of about Z0=2 [9].
The effect of the center-of-mass contribution to Z0
was found to be of the order of 40% in Refs.[24,25].
In comparison, our value of
-3 x nf x E=0.597 GeV at R=0.6 fm corresponds to
Z0=1.79 with no center-of-mass contribution.



Next: The gluonic bag constant
Up: Calculation
Previous: The canonical vacuum energy
Marc Schumann
2000-10-16
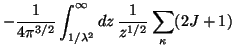
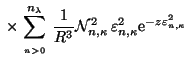
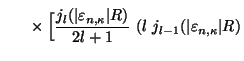
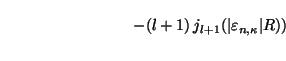
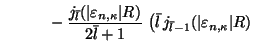
![$\displaystyle \phantom{\sum^{n_\lambda}_{\atop{n>0}}\times \Big[\frac{j_{l}(\ve...
...-
(\bar{l}+1)j_{\bar{l}+1}(\vert\varepsilon _{n,\kappa}\vert R)\right)\Big]\, .$](img34.gif)


![]()