|
|
Fracciones Continuas Generalizadas
Una nueva visión general que incluye las tradicionales fracciones
continuas, algunos ejemplos extraídos del libro: “LA QUINTA OPERACIÓN
ARITMÉTICA, Revolución del Número” ISBN: 980-07-6632-4. Copyright ©. Todos los derechos
reservados. Autor: D. Gómez.
CONTENIDO DE ESTA PAGINA:
Fracciones Continuas Generalizadas
Fracciones Fractales
Dada la ecuación algebraica f(x) = 0 de n-ésimo grado:
![]()
Su raíz de máximo modulo puede ser
expresada en términos de una fracción continua generalizada (Fracción Fractal)
de la siguiente manera:
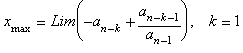
Reemplazando repetidamente la parte
fraccional por la expresión:
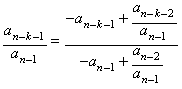
se obtiene la siguiente expresión general para la
raíz de máximo módulo de f(x):
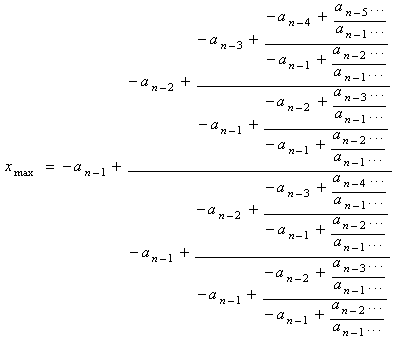
![]()
La raíz de mínimo modulo de la ecuación:
![]()
está dada por la siguiente fracción continua
generalizada:
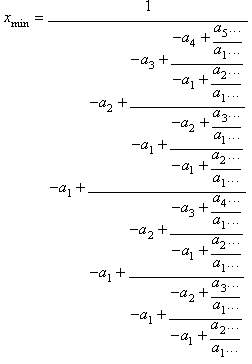
![]()
Ejemplo numérico:
Siendo a0 = -1, a1
= -2, la representación de la raíz de máximo módulo de la ecuación:
![]()
como fracción continua generalizada es:
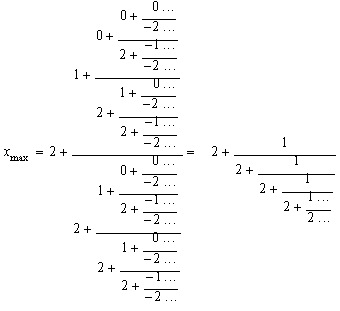
Podemos ver que la fracción continua
tradicional de el número irracional: ![]() es simplemente una expresión de segundo orden del nuevo concepto de fracción
continua generalizada.
es simplemente una expresión de segundo orden del nuevo concepto de fracción
continua generalizada.
Será necesario entonces redefinir la
tradicional representación de los números irracionales mediante
fracciones continuas. Es realmente inquietante el saber ahora que un concepto
tan elemental y general no tenga precedentes en la larga historia de las
fracciones continuas.
![]()
Otro ejemplo:
Este ejemplo fué previamente
expuesto en la lista de la Web: MATH-HISTORY LIST (3 Oct 1997)
Dada la ecuación (x+1)3 =2, o lo
mismo -x3-3x2-3x+1=0, cuya raíz de mínimo módulo es ![]() .
.
Siendo a1 = -3, a2 = -3, a3
= -1, entonces la fracción continua generalizada para esa raíz es:
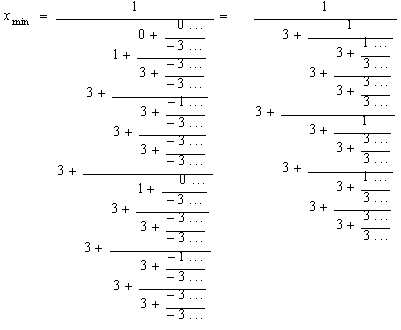
Una muy interesante expresión que ofrece una
representación periódica de un irracional cúbico. Durante mucho tiempo y bajo
la reducida visión y alcance de las tradicionales fracciones continuas se creyó
que solamente los irracionales de segundo orden es decir los irracionales
cuadráticos (raíces cuadradas) podían tener una representación periódica.
Los convergentes de esa fracción fractal son:
![]()
los cuales dan aproximaciones sucesivas al valor:
![]() .
.
Esa secuencia de convergentes está regulada por la
siguiente relación lineal homogénea de recurrencia:
yn=3yn-1
+ 3yn-2 + yn-3
Es importante notar que las fracciones continuas
generalizadas son solamente un caso especial de el Proceso Racional (Proceso
basado en la Media Racional).
Si el lector tratara de representar la raíz cúbica
de 2 mediante las fracciones continuas tradicionales (Ahora en adelante
definidas como "Fracciones continuas de segundo orden") entonces
obtendrá una representación distorsionada (coeficientes no periódicos) de ese
número irracional, así:
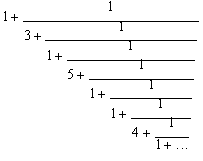
cuyos convergentes son:
![]()
![]()
Conclusiones
Resulta muy claro que las
fracciones continuas tradicionales son en realidad: "fracciones continuas
de segundo orden". Como hemos visto en los ejemplos anteriores, cuando
tratamos de representar un irracional de grado superior al segundo (raíces
cúbicas, cuartas, etc.) utilizando el concepto tradicional entonces se obtiene
una imagen distorsionada de ese irracional. Es necesario entonces redefinir
nuestro concepto acerca de la representación de los irracionales mediante
fracciones continuas.
Por otro lado es necesario tener en cuenta que las fracciones continuas
generalizadas (Fracciones fractales) son esencialmente Procesos Racionales regulados por la Media Racional.
![]()
Copyright
©
Todos los derechos reservados bajo las convenciones internacionales de
derechos de autor. Ninguna parte de estas páginas pueden ser reproducidas,
almacenadas o transmitidas en cualquier forma o por cualquier medio sin la
previa autorización del autor: D. Gómez.
Last
revision: 2002.