figure 9
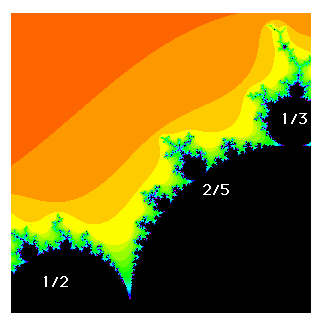
One of the most intriguing features of the primary bulbs is illustrated in Figure 9. At the top of the picture is the 1/3 bulb while at the left is the 1/2 bulb. Note that the largest bulb in between these two is the 2/5 bulb.

figure 9
Note that we obtain the largest bulb between the 1/2 and 1/3 bulbs by adding the numerators and adding the denominators; or, as the students say, by adding the fractions just the way you always wanted to add them.
In Figure 10 we have provided another example of this. The largest bulb between the 1/2 and 2/5 bulbs is the 3/7 bulb, so


figure 10
This type of addition is of course familiar from number theory: it is called Farey addition. We can produce a tree consisting of all rationals between 0 and 1 by starting with 0/1 and 1/2. Farey addition yields

which is the fraction between 0/1 and 1/1 with least denominator. Continuing, we have

which are the fractions between the two summands which again have
lowest denominators. Continuing, each stage of this process yields the
fraction between two consecutive fractions which has the smallest
denominator.
 7 The Fibonacci Sequence (Next Section)
7 The Fibonacci Sequence (Next Section) Fractal Geometry of the Mandelbrot Set (Cover Page)
Fractal Geometry of the Mandelbrot Set (Cover Page) 5 How to Count (Previous Section)
5 How to Count (Previous Section)