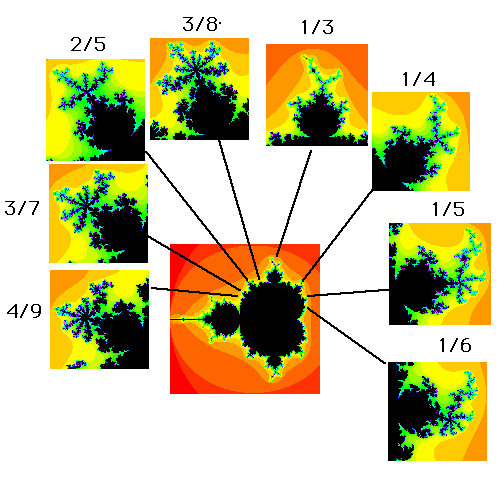
Figure 7
Now let's use the rotation numbers to investigate the arrangement of the bulbs around the main cardioid. This is one of the main experiments performed in the chaos club. The idea is to use the computer to determine experimentally the location of the p/q bulbs for q between 2 and 7. A number of these are sketched in Figure 7. Note that the bulbs are ordered exactly as the rational numbers! The fact is that there is a unique p/q bulb for each rational between 0 and 1 and these fractions are ordered in the natural way around the cardioid (beginning at 0 at the cusp and proceeding in a counterclockwise direction around the boundary ending at 1, again at the cusp). That is, the Mandelbrot set serves as a real number line (or at least a rational number line). Moreover, unlike the real line, each number on M can be clearly identified by looking at the antennas and counting the spokes.

Figure 7
The reason why this is true demands a bit of complex calculus. Recall that the fixed points of Fc are given by the roots of x2 + c = x which are
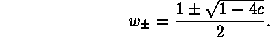
We have
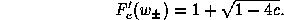
Along the boundary of the main cardioid, we saw earlier that
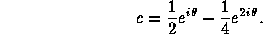
As 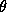 increases from 0 to
2 Pi, c travels once around the
boundary of the cardioid in the counterclockwise direction. It follows
that the fixed points are given by
increases from 0 to
2 Pi, c travels once around the
boundary of the cardioid in the counterclockwise direction. It follows
that the fixed points are given by

when c lies on the boundary. Note that
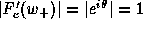
so that 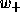 is a neutral fixed
point. If we were to compute the value of
is a neutral fixed
point. If we were to compute the value of 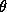 at the point where
the p/q bulb attaches to the main cardioid, then it is a fact that
at the point where
the p/q bulb attaches to the main cardioid, then it is a fact that
What happens is a fixed point and a period q point coalesce into a neutral fixed point whose derivative is
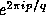 .
.
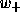 (at
least infinitesimally). When c is in the p/q bulb, this fixed
point is now repelling while the cycle becomes attracting and inherits
the rotation. A "movie'' of this is shown for the 1/3 bulb in Figure
8.
(at
least infinitesimally). When c is in the p/q bulb, this fixed
point is now repelling while the cycle becomes attracting and inherits
the rotation. A "movie'' of this is shown for the 1/3 bulb in Figure
8.
Figure 8. A movie of the attracting cycle in the 1/3 bulb.
 6 How to Add (Next Section)
6 How to Add (Next Section) Fractal Geometry of the Mandelbrot Set (Cover Page)
Fractal Geometry of the Mandelbrot Set (Cover Page) 4 Rotation Numbers (Previous Section)
4 Rotation Numbers (Previous Section)