Jacobi's and Gauss-Seidel Method

Let and (i = 1 : n). We will consider the solution of the system of equations
 
by an iterative method.

Definition 7.2.1. The approximation or the approximate value of the solution of system (1) is a vector that in certain sense differs little from the vector Let us represent system (1) in the form

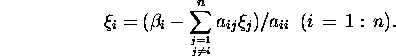
Jacobi's iterative process is defined by the algorithm
 
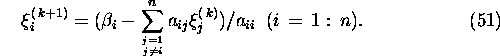
The Gauss-Seidel iterative process is defined by the algorithm
 
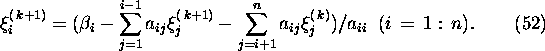
In case of both Jacobi's and the Gauss-Seidel iterative processes the transition from the approximation of the solution of system (1) to the next approximation can be described using the matrices

and while A=L+D+U. For example, Jacobi's algorithm can be represented as
 
where M_J=D and N_J=-(L+U). The Gauss-Seidel algorithm (3) can be represented as
 
where M_G=D+L and N_G=-U.

Example 7.2.1.^* Let us solve the system , where

by Jacobi's method.
Let us represent the matrix A in the form

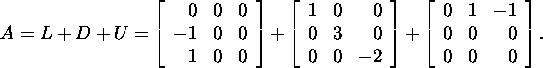
We will form the matrices M_j and N_j:

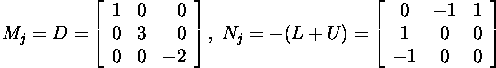
The algorithm of Jacobi's iterative process can be given in the form

Since

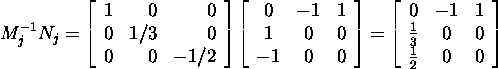
and

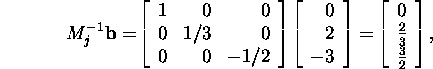
then

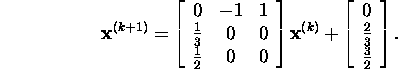
If we take for the initial approximation then we shall have



:





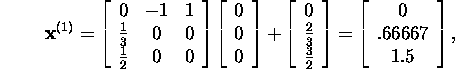
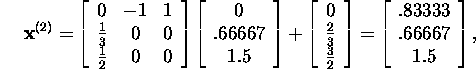
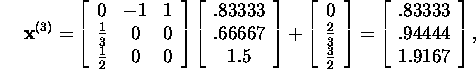
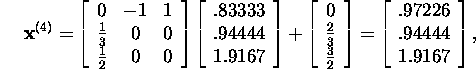
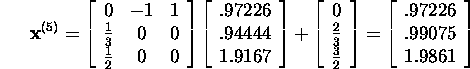
and so on (the exact solution of this equation is ).

Problem 7.2.1.^* Solve the system given in example 7.2.1 by the Gauss-Seidel method.