Algorithm 3.3.1. To find the singular
value decomposition of the matrix 
one has to:
I Find the eigenvalues of
the matrix ATA and arrange them in descending order.
II Find the number of nonzero eigenvalues
of the matrix ATA.
III Find the orthogonal eigenvectors
of the matrix ATA corresponding to the obtained eigenvalues,
and arrange them in the same order to form the column-vectors of the matrix
.
IV Form a diagonal matrix 
placing on the leading diagonal of it the square roots 
of 
first eigenvalues of the matrix
ATA got in I in descending order.
V Find the first column-vectors of the matrix 
:
VI Add to the matrix U the rest of m-r vectors using
the Gram-Schmidt orthogonalization
process. 
Example 3.3.1. Let
us find the singular value decomposition
of the matrix
I Find the eigenvalues of the matrix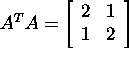 
:
II Find the number of nonzero eigenvalues
of the matrix ATA: r=2.
III Find the orthonormal eigenvectors
of the matrix ATA corresponding to the
eigenvalues 
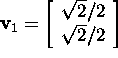and 
:
and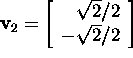 
forming a matrix
IV Find the singular value matrix
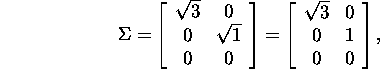
on the leading diagonal of which are the square roots of the eigenvalues
of the matrix ATA (in descending order) and the rest
of the entries of the matrix 
are zeros.
V Find the first two column-vectors of the matrix 
using the formula (9)
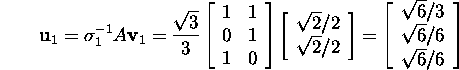
and
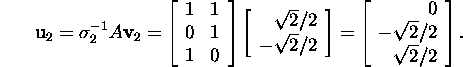
VI To find the vector 
we shall first find, applying the Gram-Schmitd
process, a vector 
perpendicular to 
and 
:
Norming the vector 
we get
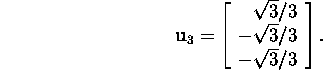
Hence
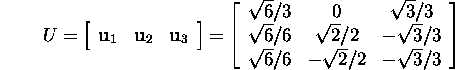
and the singular value decomposition of the matrix A is
Example 3.3.2. Let
us find the singular value decomposition
of the matrix 
.
I Find the eigenvalues of
the matrix ATA:
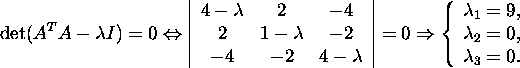
II Find the number of the nonzero eigenvalues
of the matrix ATA: r=1.
III Find the eigenvector of
the matrix ATA:
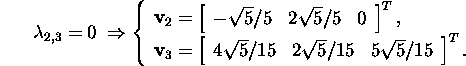
Since the eigenvalue 0 is multiple, the Gram-Schmidt
orthogonalization process is used to find the vector 
.
We compile the orthonormal matrix V:
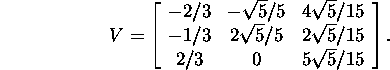
IV Form the singular value matrix:
V Calculate the unique column-vector of the matrix U applying the
formula (9):
Thus the singular value decomposition
of the matrix A is
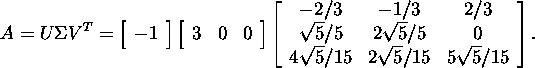
Example 3.3.3.*
Let us find the singular value
decomposition of the matrix
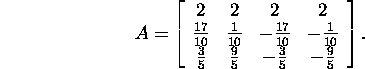
The given 
matrix A has utterly three nonzero singular
values. Therefore it is suitable to find nonzero singular
values of the matrix A using the 
matrix AAT (not the 
matrix ATA). Since
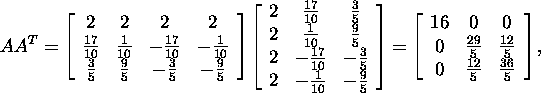
then the characteristic
equation of AAT is
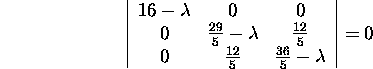
or
and the solutions of this equation are 
and 
Since 
and the matrix
is a
matrix, then on the leading diagonal of the matrix
there are the singular values
of the matrix A in descending order, and all other elements of the
matrix
are zeros:
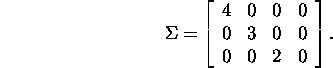
The matrix U has for column-vectors the orthonormed eigenvectors
of the matrix AAT:
Collecting the vectors 
and 
we obtain the matrix
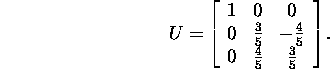
According to the relation (6), we shall find
the first three column-vectors of the matrix V (the matrix
has on its leading diagonal three nonzero entries) using the formula
Hence
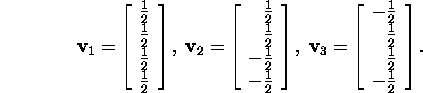
To calculate the vector 
,
we find first, using the Gram-Schmitd
orthogonalization process, the vector 
perpendicular to the vectors 
and :
Since 
then
and
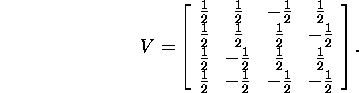
Let us check the result:
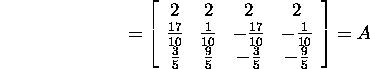
and
:
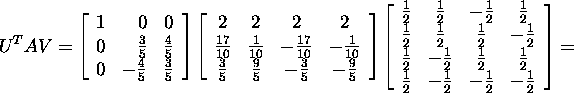
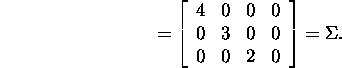
Problem 3.3.1.* Applying the singular
value decomposition of the matrix A got in example
3.3.3, find the bases of the
subspace of the column-vectors
the right null space 
the subspace of the row-vectors
,
and the left null space
of the matrix A.
Problem 3.3.2.* Find the singular
value decomposition and the QR
factorization of the matrix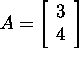 
.
Problem 3.3.3.* Find the singular
value decomposition of the matrix 
.