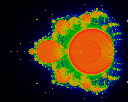
 Average age. That is, cycles at which pixel was hit were accumulated,
and then normalized by the measure at that pixel.
Average age. That is, cycles at which pixel was hit were accumulated,
and then normalized by the measure at that pixel.
 Hausdorf measure of Mandelbrot Interior. Red outline shows
boundary of set, as usually seen.
Hausdorf measure of Mandelbrot Interior. Red outline shows
boundary of set, as usually seen.
 Average age. That is, cycles at which pixel was hit were accumulated,
and then normalized by the measure at that pixel.
Average age. That is, cycles at which pixel was hit were accumulated,
and then normalized by the measure at that pixel.
 Very high iterations ... allowed to iterate a far, far longer time.
Note that some of the "fuzz" in "fine" is cleaned up.
Very high iterations ... allowed to iterate a far, far longer time.
Note that some of the "fuzz" in "fine" is cleaned up.
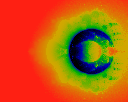 Square distance between iterations; i.e (x-xlast)^2 + (y-ylast)^2
acumulated and normalized.
Square distance between iterations; i.e (x-xlast)^2 + (y-ylast)^2
acumulated and normalized.
 Gaussian edge filter applied to above.
Gaussian edge filter applied to above.
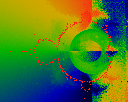 Average orientation (angle) of jump, where a "jump" is the vector from
the last to the current location. That is,
phi = arctan ((y-ylast)/(x-xlast)) accumualted and normalized.
Average orientation (angle) of jump, where a "jump" is the vector from
the last to the current location. That is,
phi = arctan ((y-ylast)/(x-xlast)) accumualted and normalized.
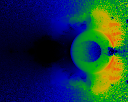 Cosine of angle between current jump and last jump. The colormap used
shows black = 0.0 (angle=90), red=1.0 (angle = 0).
This is a very nice spirit-catcher, on it's side.
Cosine of angle between current jump and last jump. The colormap used
shows black = 0.0 (angle=90), red=1.0 (angle = 0).
This is a very nice spirit-catcher, on it's side.
 A different colormap brings out different detail.
A different colormap brings out different detail.
 Average X origin. The is, each pixel shows the average value of the
real part of C where z = z^2+C.
Average X origin. The is, each pixel shows the average value of the
real part of C where z = z^2+C.
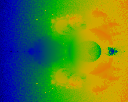 Average Y origin. The is, each pixel shows the average value of the
imaginary part of C where z = z^2+C.
Average Y origin. The is, each pixel shows the average value of the
imaginary part of C where z = z^2+C.
 Edge detection applied to average X origin.
Edge detection applied to average X origin.
 Edge detection applied to average Y origin.
Edge detection applied to average Y origin.
 Curl (dxY - dyX) of the average origin (X, Y). Curiously, the
Divergence (dxX + dyY) looks qualitatively similar.
Curl (dxY - dyX) of the average origin (X, Y). Curiously, the
Divergence (dxX + dyY) looks qualitatively similar.
 Curl, as above, but with slightly different colormap.
Curl, as above, but with slightly different colormap.
 Divergence. Note qualitative similarities, and subtle differences (which
help reveal some of the minute artifacts in the other images).
Divergence. Note qualitative similarities, and subtle differences (which
help reveal some of the minute artifacts in the other images).
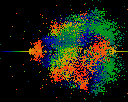 Splat. Just a splat. Note the spiral structure, bottom center. How to
clean this up ??
Splat. Just a splat. Note the spiral structure, bottom center. How to
clean this up ??
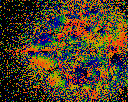 Origins -- X. That is, each point is colored with the real part of C where
z = z^2 + C. Unlike the average origins image above, this is done with
a "last point wins" coloring.
Origins -- X. That is, each point is colored with the real part of C where
z = z^2 + C. Unlike the average origins image above, this is done with
a "last point wins" coloring.
 Fine origins -- X. As above, but different colormap.
Fine origins -- X. As above, but different colormap.
The first image was created in 1988, as were variations on some of the others. All electronic copies were lost, with only polaroids and proof sheets surviving. New electronic copies were recreated in 1996 for this web exhibit.
Copyright (c) 1988, 1990, 1996 Linas Vepstas