Hacked Mandelbrot

Here is the usual Mandelbrot set, z(n+1) = z(n)*z(n) + c, where c = K * exp (i*theta). Well, we've plotted theta along x-axis, and K along y axis. K runs from 0.0 to 2.0, and theta from 0 to 2*pi.

Well, the base looks pretty darn circular, right? Its not. It's ever so slightly eccentric (nothing in life is easy). The shape is given by the often quoted "cardiod", z = 0.5 * exp (i*phi) - 0.25 * exp (2*i*phi), which, in our coordinate system, K = 0.5 * sqrt (1.25 - cos(phi)) and theta = arctan ( (sin(phi) - 0.5*sin(phi)) / (cos(phi) - 0.5*cos(phi))). In this coordinate system, the cardiod is very nearly a circle, a fact that has pained me greatly.

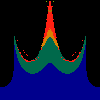
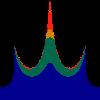
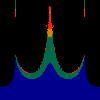
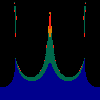
Now we start playing some distortion games. The images below represent the usual iteration, except that now, we start playing with the strength of the cross term. That is, instead of the usual

z <-- z*z + c  
   == (x+i*y)*(x+i*y)  + Re(c) + i*Im(c)
   == x*x - y*y + Re(c)  + i * (2*x*y + Im(c))

we play with the cross term ...

z <-- z*z + c  
   == (x+i*y)*(x+i*y)  + Re(c) + i*Im(c)
   == x*x - y*y + Re(c)  + i * (2*x*y(1.0-lambda) + Im(c))

In the sequence below, we see lambda go from 0.1 to 1.0, in steps of 0.1. Click on the prictures with the big borders.

In this next sequence, we have lambda from -0.1 to -1.5 in steps of 0.1