The Farey Room

The Farey Room contains pictures of transformations of the Farey Number Mapping (Farey Tree), and through transformations of the Continued Fraction Mapping. Some of the theory behind these pictures is developed in the following papers:

Continued Fractions and Gaps explores the nature and distribution of the fractally-distrubted cleavages in these images.
Symmetries of Period-Doubling Maps identifies the Modular Group SL(2,Z) as the basic symmetry group of the cleavages.
The Bernoulli Map, the Gauss-Kuzmin-Wirsing Operator and the Riemann Zeta shows a relationship between fractals and the Riemann Zeta.
The Minkowski Question Mark and the Modular Group SL(2,Z) shows that the distribution of Farey Fractions transforms under the dyadic representation of the Modular Group.

Please see also the newer, nicer version of this web page.

Continued Fractions

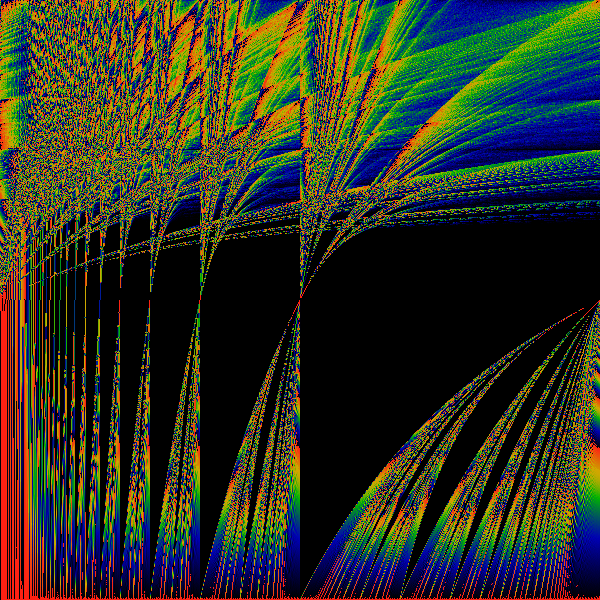
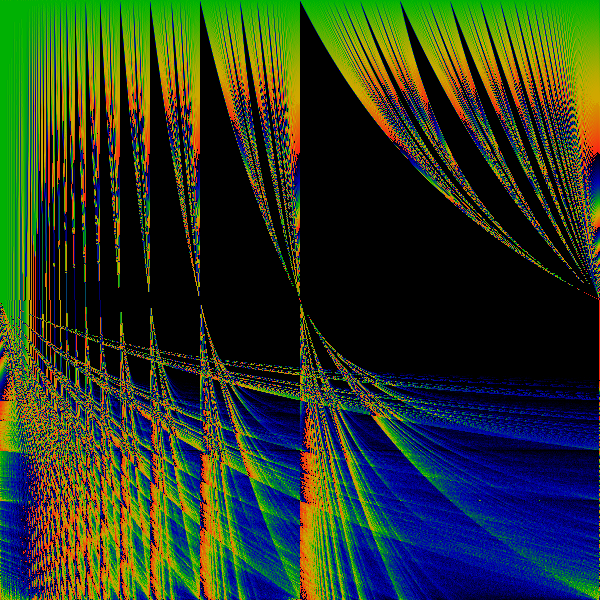
iterated eqn.

The above shows the most basic transformation, where all occurances of "1" in the numerator of continued fraction expansions of the real number are replaced by "z". That is, if x = 1/(a+1/(b+1/(c+1/(d+ ...)))) then f(x) = z/(a+z/(b+z/(c+z/(d+ ... )))) mod 1. This f(x) is used to generate a Hausdorff measure for a given (x,z). The measure is shown as a color, with black=zero, blue=small, green=larger, yellow=large, red=larger still. Note that as z gets larger than one, it is technically undefined, as the continued fraction rockets out of control. However, computationally, x was always a rational (but barely ...), and so each continued fraction terminates. Along the horizontal axis, real numbers. Along the vertical axis, z, ranging from 0 to 2.

Note the psuedo-Arnold's Tongues which occur for all irrational values on the horizonal axis. This is essentially due to the fact that the mapping is discontinuous for all rational values. A cross-section of this picture (a horizontal line drawn through it) is a Cantor set.

iterated eqn.

Cosine Transform 1 -> cos (z)

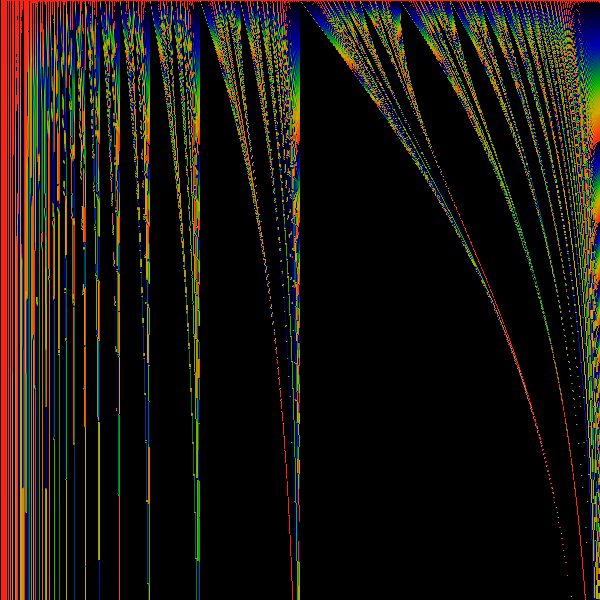
iterated eqn.

Exponential Transform 1 -> exp (z)

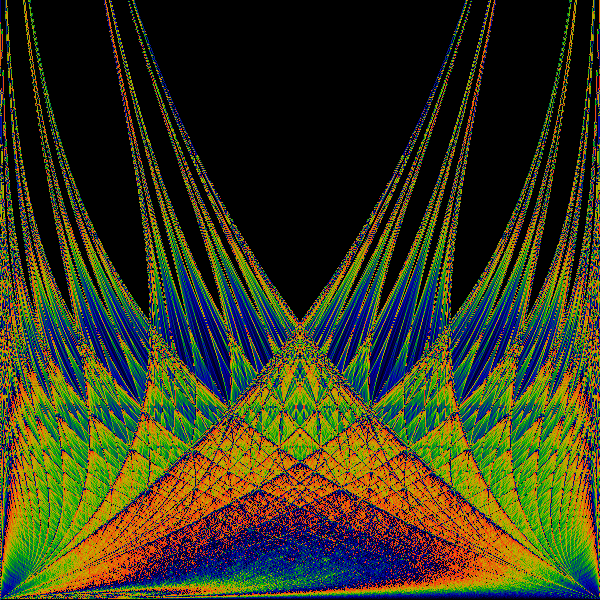
iterated eqn.

An attempt to create a symmetrized version

iterated eqn.

Spherical Bessel (j0) Transform 1 -> j0(z)

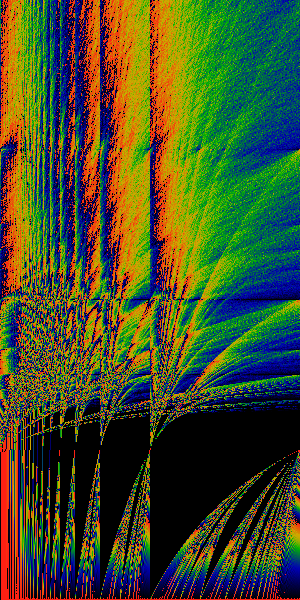
iterated eqn.

Tall

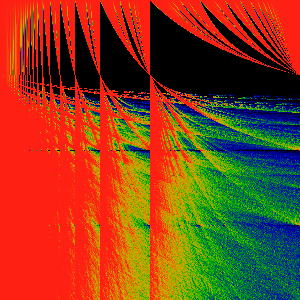
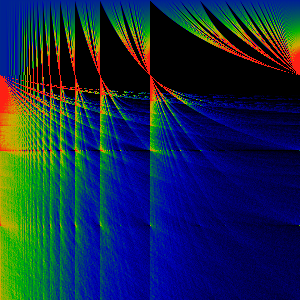
iterated eqn. Wide

iterated eqn.

Farey Transforms

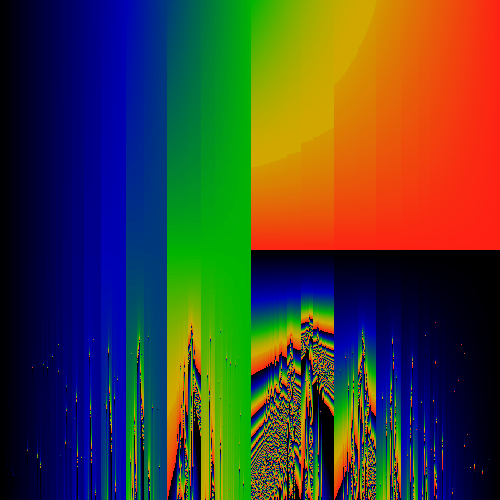
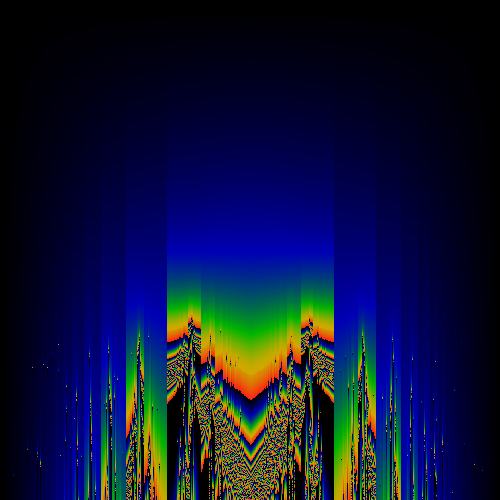
iterated eqn.

Symmetric component of above image

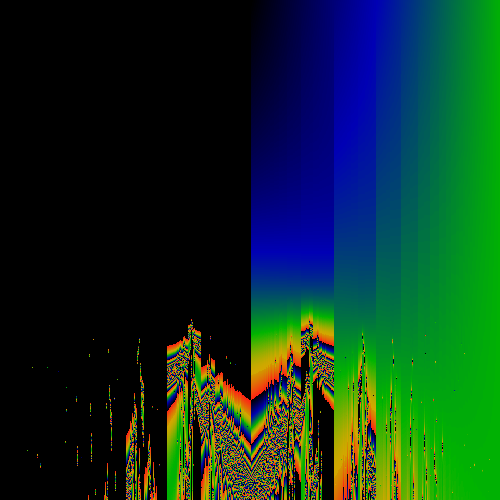
Anti-symmetric component of above image

Most of these images were generated during January and February of 1994, in Austin, Texas. The work was inspired by a Christmas reading of the "Contorted Fractions" chapter of John Conway's "On Numbers and Games".

Linas Vepstas February 1994

References

Stern-Brocot Tree
The Minkowski Question Mark provides another important bridge between Farey Trees and Fractals.

The quickie bibliography below was scammed from http://www.math.uwn.edu/Farey.html

J.C. Lagarias and C. Tresser, A walk along the branches of the extended Farey tree, IBM Jour. of Res. and Dev., v. 39, 1995.
J.C. Lagarias, Number theory and dynamical systems, Proceedings of Symposia in Applied Mathematics 46, 35-72, 1992.
R. Siegel, C. Tresser, and G. Zettler, A decoding problem in dynamics and in number theory, Chaos 2, 473-493, 1992.
G.H. Hardy and E.M. Wright, An introduction to the theory of numbers, fifth edition, Clarendon, Oxford, England, 1979.
J. Farey, On a curious property of vulgar fractions, Philos. Mag. & Journal, London 47, 385-386, 1816.
Anonymous author, On vulgar fractions, Philos. Mag. & Journal, London 48, 204, 1816.
J. Farey, Propriété curieuse des Fractions Ordinaires, Bull. Sc. Soc. Philomatique 3, No. 3, 112, 1816.
J. Franel, Les Suites de Farey et le Problémes des Nombres Premiers, Gottinger Nachrichten, pp. 198-201, 1924.
P. Cvitanovi\'c, Farey Organization of the fractal hall effect, Phys. Scripta T9, 202, 1985.
P. Cvitanovi\'c, B. Shraiman, and B. Söderberg, Scaling laws for mode locking in circle maps, Phys. Scripta 32, 263-270, 1985.

The Farey Room by Linas Vepstas is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.