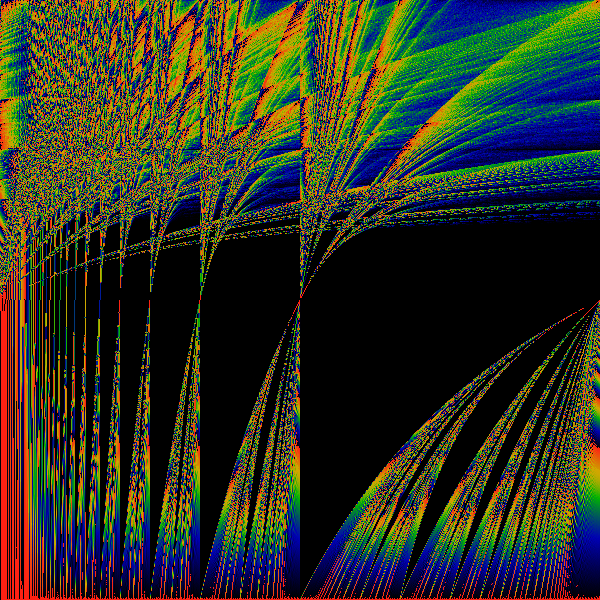

The above shows the most basic transformation, where all occurances of "1" in the numerator of continued fraction expansions of the real number are replaced by "z". That is, if x = 1/(a+1/(b+1/(c+1/(d+ ...)))) then f(x) = z/(a+z/(b+z/(c+z/(d+ ... )))) mod 1. This f(x) is used to generate a Hausdorff measure for a given (x,z). The measure is shown as a color, with black=zero, blue=small, green=larger, yellow=large, red=larger still. Note that as z gets larger than one, it is technically undefined, as the continued fraction rockets out of control. However, computationally, x was always a rational (but barely ...), and so each continued fraction terminates. Along the horizontal axis, real numbers. Along the vertical axis, z, ranging from 0 to 2.
Note the psuedo-Sinai's Tongues which occur for all irrational values on the horizonal axis. This is essentially due to the fact that the mapping is discontinuous for all rational values.

Cosine Transform 1 -> cos (z)
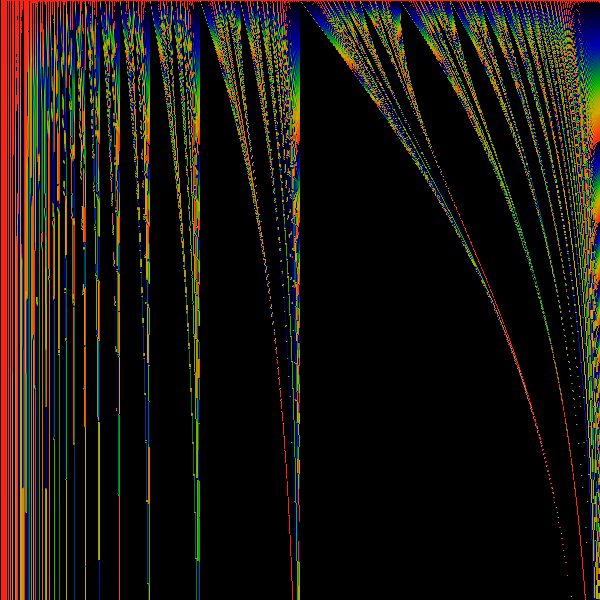
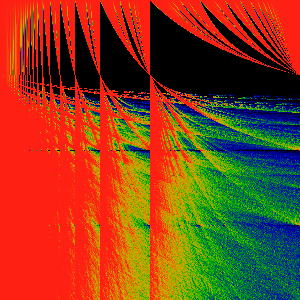
Exponential Transform 1 -> exp (z)
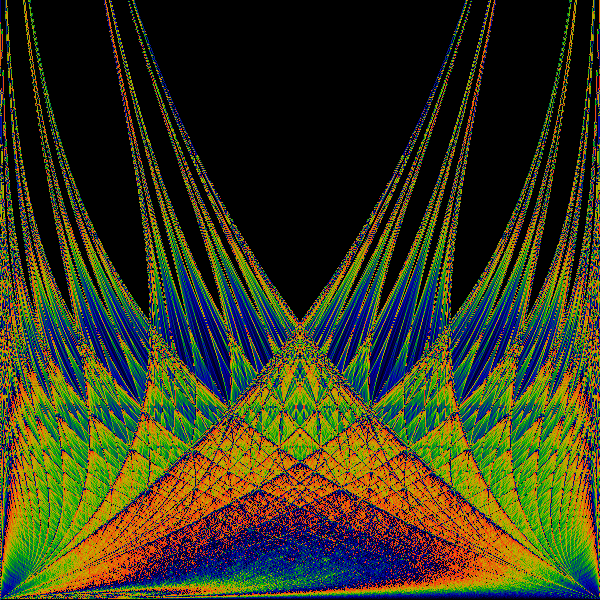
An attempt to create a symmetrized version

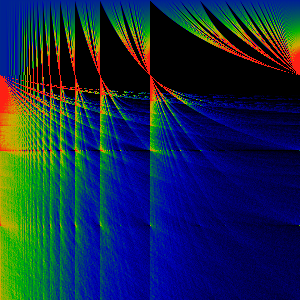
Spherical Bessel (j0) Transform 1 -> j0(z)
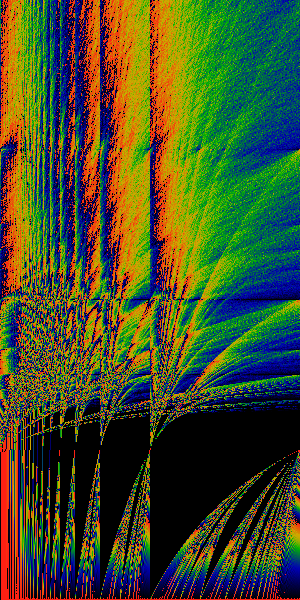
Tall
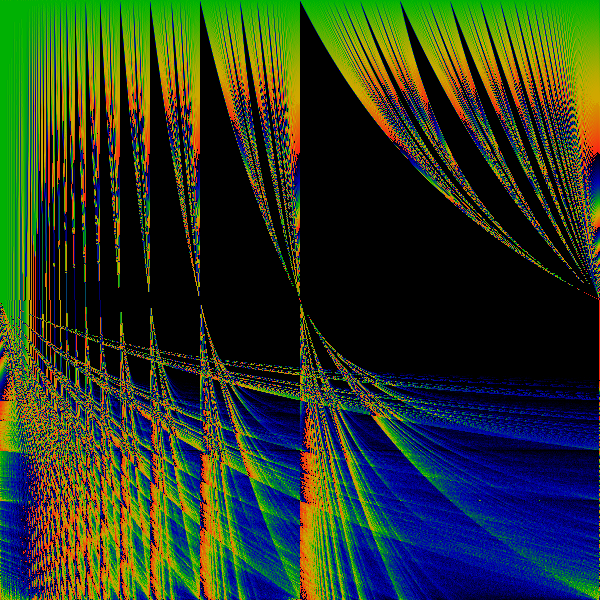 Wide
Wide
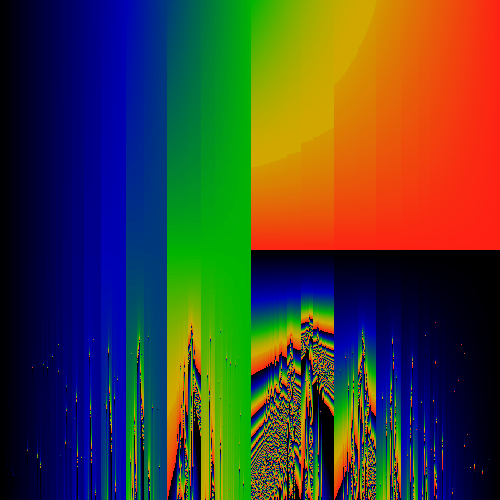
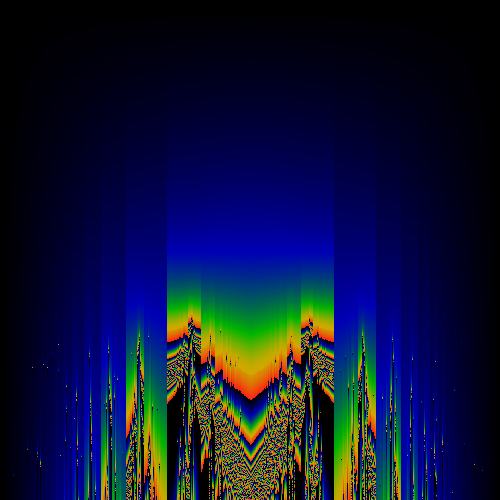
Symmetric component of above image
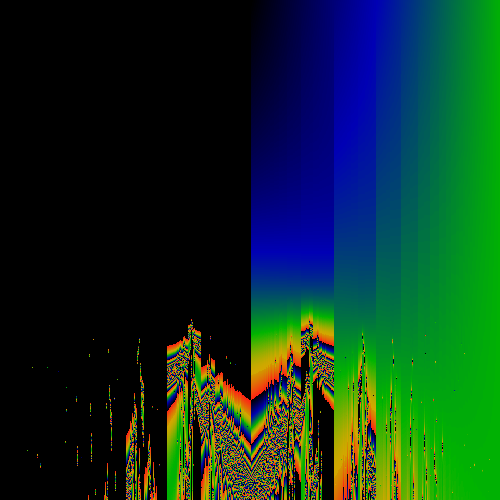
Anti-symmetric component of above image
Linas Vepstas February 1994