Renormalizing the Mandelbrot Escape
Anyone who has ever scratched the surface of the Mandelbrot set knows
that it involves counting to infinity. Counting to infinity is rarely
a light undertaking, and doing so often leaves the counter unsatisfied.
For those imaging the Mandelbrot Set, this count is usually avoided by
introducing the concepts of "maximum iterations" and an "escape radius".
The technically minded often wonder what a change in the escape radius
will do; while the artistically minded cannot help but notice that the
number of iterations until escape is an integer, resulting in a
stair-step function that is not always visually appealing.
It is not widely known that a smooth fractional iteration count can be
defined and easily applied. Its definition is not at all difficult;
the theory behind it, however, is a bit mathematical at times.
We present one derivation, and some results below. An alternate
derivation, using the technique of
Spectral Analysis of Eigenvalues in Hilbert spaces,
is here.
Spectral analysis allows one to define a unique, smooth, invariant
fractional iteration count that accurately describes the result of
counting (with integers!) until infinity.
The smooth iteration count has several uses, not the least of which is
the generation of nice, smooth pictures, as shown below. Another
utility comes through its close connection to the
Douady-Hubbard potential and external rays.
The Theory
Consider the traditional iterated Mandelbrot Set equation:
int iter_count = 0;
float escape_radius = 20.0;
complex Z, C;
loop (forever) {
Z = Z*Z +C;
iter_count ++;
float modulus = sqrt (ReZ*ReZ + ImZ*ImZ);
if (modulus > escape_radius) goto stop;
if (iter_count > maxiter) goto stop;
}
stop:
color_value = colormap_lookup (iter_count);
draw_pixel;
It can be clearly seen that the iteration count in this traditional
algorithm is integer-valued, and that the actual value depends on the
choice of the escape radius.
The scale-dependence on the escape radius can be (partly) removed
by differentiating the above formula with respect to the escape radius,
taking the limit to infinity, and then integrating the first term of the
resulting differential equation. The result is a renormalized,
scale-independent, quasi-integral-valued iteration count:
m = iter_count - log (log escape_radius) /log 2
In the above, m still changes by integer values; however, it
can be seen that it is roughly independent of the escape radius:
increasing the escape radius will on average increase the iteration count
as well, and the two will cancel each other out.
Next, let's look for the fractional iteration count. As the escaped
values of Z are iterated and diverge to infinity, the behavior
eventually becomes quite simple: Z(n) = X ^ 2 ^ n for some
value of X. The dependence on n is simple; the dependence of Z
on n can be gotten by taking the logarithm. In a fashion similar to
that above, we can deduce that
1 > m + log (log |X|) / log 2 > 0
where m is the renormalized iteration count above, and |X| is the
modulus of the complex-number valued X in the equation above.
It is now a simple matter to put these two terms together to obtain the
fully-renormalized fractional iteration count:
mu = m + frac = n + 1 - log (log |Z(n)|) / log 2
where n is the number of iterations needed to exceed the escape
radius, and |Z(n)| is the modulus of the iterate just after it
escapes. That is, |Z(n)| > R > |Z(n-1)| were R
is the escape radius.
In the above formula, the value of mu is almost completely
independent
of the iteration count, and of the escape radius, despite the fact that
the right-hand-side of the equation is explicitly dependent on both of
these quantities. The renormalized iteration count mu depends
only on C, and is a piecewise-continuous, differentiable function
thereof. By using a different analysis, it can be seen that the
renormalized iteration count mu is in fact the residue
remaining when a pole (due to the infinite sum) is removed. That is,
the value of mu closely approximates the result of having
iterated to infinity, that is, of having an infinite escape radius,
and an infinite max_iter.
The formula above is clearly numerically tractable, and can be
easily coded up into a computer program, without presenting any special
challenges whatsoever. Some sample results are shown below.
The function above is discontinuous; the locations of the discontinuities
are shown in the bottom-most figure below. An estimate of the
size of the discontinuity is easily computed. Consider a value of
C such that |Z(n)| = R - epsilon. Then
mu(R) = n + 1 - log log |Z(n)^2 +C| / log 2
and
mu(R-2*epsilon) = n - log log |Z(n)| / log 2
For |Z(n)| > > |C|, we have
|Z(n)^2 + C| = |Z(n)|^2 * (1 + Re (C/Z(n)^2))
thus yielding
mu(R) - mu(R-2*epsilon) = Re ( C / (Z(n)*Z(n)) ) / ( 2 * log |Z(n)| * log (2) )
Although the above indicates that the error term decreases quadratically
as the escape radius is increases, it is important to note that
the error term decreases as a double-exponential of the number of iterations past
the escape radius. That is, if instead of the mu defined above, we
use the formula
mu' = n + 5 - log (log |Z(n+4)|) / log 2
and an escape radius of 10, then the error is approximately
one part in 1.0e32 -- miniscule indeed, and with each additional
iteration shrinking by a square again.
The author has attempted vainly, and in vain, to discover
the continuous-everywhere analogue of mu. However,
this appears to be more difficult than it first appears, even
as it appears to be tantalizingly simple. Note that a series
expansion of additional correction terms is possible (these
terms contain factors of the form Re (c/z^2)) but tedious.
Indeed, the same results can be far more easily achieved simply
by iterating few more times! Due to the extremely rapid
convergence that is possible by iterating a few more times,
a series expansion makes no sense.
A different derivation of the above results, using regulated sums,
lies here.
Iterating Different Equations
The above formulas apply only to the Mandelbrot iterate. Other iterates
require modified equations. The corresponding results are easy to get.
If the iterated equation is of the form
Z(n) = Z(n-1) ^ p + lower-power-terms
where ^ denotes exponentiation, and p is the highest
power of Z occurring in the iterated equation, then
mu = n + 1 - log (log |Z(n)|) / log p
A Simplified Explanation
The following simplified and very insightful explanation is
provided by Earl L. Hinrichs:
"Ignoring the +C in the usual formula, the orbit point grows by
Z := Z^2. So we have the progression
Z, Z^2, Z^4, Z^8, Z^16, etc. Iteration counting
amounts to assigning an integer to these values. Ignoring
a multiplier, the log of this sequence is: 1, 2, 4, 8, 16.
The log-log is 0, 1, 2, 3, 4 which matches the integer value
from the iteration counting. So the appropriate generalization
of the discrete iteration counting to a continuous function
would be the double log."
This simplified explanation also provides a simple insight into
why a division by the logarithm of the power is required: consider
iterating Z := Z^3. The log of the sequence yields
1, 3, 9, 27, 81, 243 ... and the double-log yields
0, log(3), 2log(3), 3log(3), 4log(3), ....
The Revised Algorithm
Just to make it clear what these formulas mean, we present the revised
algorithm that employs them. Only two lines are changed:
int iter_count = 0;
float escape_radius = 20.0;
complex Z, C;
loop (forever) {
Z = Z*Z +C;
iter_count ++;
float modulus = sqrt (ReZ*ReZ + ImZ*ImZ);
if (modulus > escape_radius) goto stop;
if (iter_count > maxiter) goto stop;
}
stop:
Z = Z*Z +C; iter_count ++; // a couple of extra iterations helps
Z = Z*Z +C; iter_count ++; // decrease the size of the error term.
float modulus = sqrt (ReZ*ReZ + ImZ*ImZ);
float mu = iter_count - (log (log (modulus)))/ log (2.0);
color_value = colormap_lookup (mu);
draw_pixel (C, color_value);
Test Results & Images
Below follow some test images illustrating the technique.
All of the images were created with the intentionally small
max-iter of 18, resulting in spatially low-res images. The point is
that such a low max-iter does not limit one to a mere 18 colors for the
colormap, and that the technique really does produce a very smooth
fractional escape value.
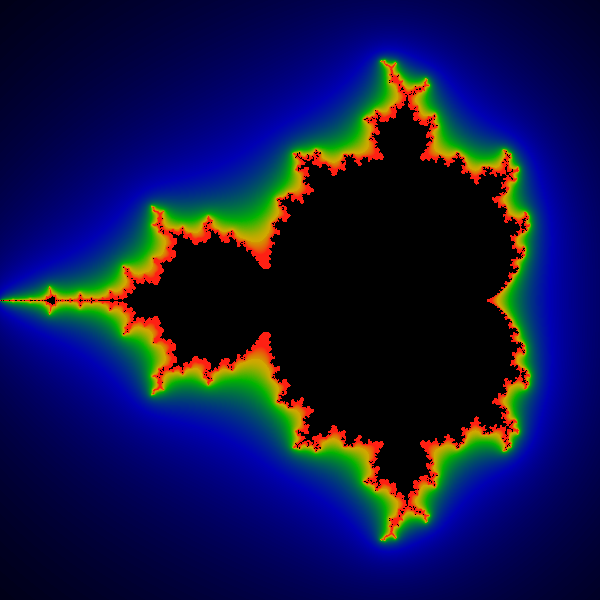
Radius of 2.1e10. The above shows the results with a
maxiter=18 and an escape radius of 2.1e10 -- i.e. 21 billion.
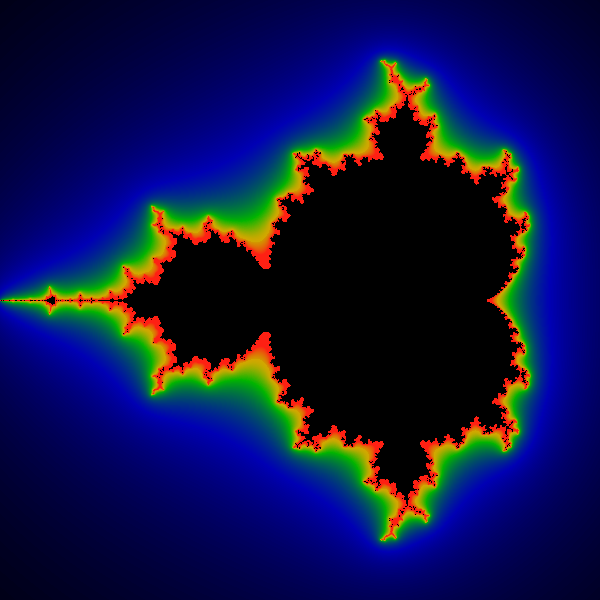
Radius of 2.1e3. The above shows the results with a
maxiter=18 and an escape radius of 2,100 -- two thousand, one
hundred. Note that this picture is visually indistinguishable
from the above.

Radius of 3.1. The above shows the results with a
maxiter=18 and an escape radius of 3.1 -- three.
Note that this picture is visually indistinguishable
from the above.

Error Term. The above image is a difference between the
r=20 and r=2000 images, magnified by one-thousand. Clearly, it appears
that the error is bounded by approx one part in a thousand for escape
radii in this range. Visually speaking, the error term is invisible to
the naked eye.
References:
This page:
http://linas.org/art-gallery/escape/escape.html
A simplified presentation for the Fractal Art FAQ:
http://linas.org/art-gallery/escape/escape.html
Derivation of same results via Spectral Analysis:
http://linas.org/art-gallery/escape/math.html
Douady-Hubbard Potential:
http://linas.org/art-gallery/escape/ray.html
The Fractal Art FAQ:
http://www.mta.ca/~mctaylor/sci.fractals-faq/
Created by Linas Vepstas 1 June 1997
linas@linas.org
Return to Linas' Art Gallery
Copyright (c) 1997 Linas Vepstas.

Renormalizing the Mandelbrot Escape
by Linas Vepstas is licensed under a
Creative Commons
Attribution-ShareAlike 4.0 International License.




