The boundary of this region consists of c values for which the magnitude of this derivative is 1, i.e., for c-values for which
Solving the equations above using this fact yields
which parametrizes a cardioid as t runs from 0 to 2 pi. Similarly, the large disk to the left of the main cardioid consists of c-values for which Fc has an attracting cycle of period 2. One may easily check that this region is bounded by the circle of radius 1/4 centered at c = -1.
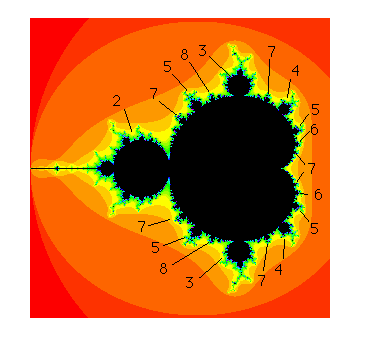
Figure 2. Periods of the bulbs in M
The primary bulbs in M are those decorations that are directly attached to the main cardioid. In the sequel we will be mainly concerned with these decorations.
Recall from [7] that we may also read off the period of the primary bulbs by simply counting the spokes of the antenna attached to this decoration. Note that each bulb features a large antenna that contains a junction point from which a number of spokes emanate. It is a fact that the number of these spokes is exactly the period of the bulb. When counting these spokes, it is important to count the main spoke (the spoke that is attached directly to the bulb). For example, in Figure 3 we have displayed several of the primary decorations and their periods.
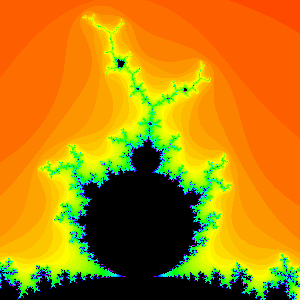 Period 3
Period 3
 Period 9
Period 9
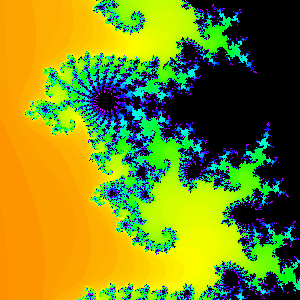 Period 19
Period 19
Figure 3.
There is another way to read off the period of the primary bulbs. Choose any c in the interior of such a bulb and compute Jc. Of course, Jc is a connected set. However, there are infinitely many points in Jc that have the property that Jc becomes disconnected whenever any one of these points is removed. In fact, when such a point p is removed, Jc always separates into n disjoint pieces where n is the period of the primary bulb containing c. The word primary is important here. See Figure 4.

Figure 4
 4 Rotation Numbers (Next Section)
4 Rotation Numbers (Next Section) Fractal Geometry of the Mandelbrot Set (Cover Page)
Fractal Geometry of the Mandelbrot Set (Cover Page) 2 Role of the Critical Orbit (Previous Section)
2 Role of the Critical Orbit (Previous Section)