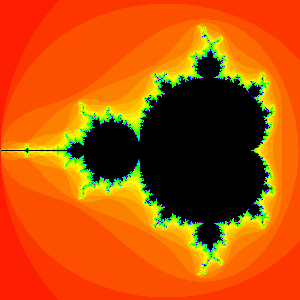
Figure 1. The Mandelbrot set.
The Mandelbrot set is the parameter space for the iteration of the quadratic family of maps FC(x) = x2 + c. Here both x and c are complex numbers. Given a seed x0, the orbit of x0 is the sequence x0, x1, x2,...> where
xn+1 = Fc(xn)
Of particular interest is the orbit of 0, the critical orbit. The Mandelbrot set consists of all c-values for which the critical orbit is bounded. We denote the Mandelbrot set by M. See Figure 1. For example, c = i lies in the Mandelbrot set since the critical orbit for Fi is
which eventually cycles with period 2. On the other hand, c = 2i does not lie in M since the critical orbit for F2i is
and it is easy to check that this orbit tends to infinity.

Figure 1. The Mandelbrot set.
A closely related object is the filled Julia set of x2 + c. This set, denoted Jc , consists of all seeds whose orbits remain bounded under iteration of x2 + c. For example, J0 is the closed unit disk centered at the origin in the plane. Indeed, if x0 = r exp(it), then
so the orbit of x0 escapes if and only if r>1.
In general, Jc is a much more complicated set; its boundary is a fractal (unless c = 0 or c = -2). To compute Jc, we make use of the fact that
provided that
Thus any orbit that eventually leaves the both the circle of radius 2 and of radius |c| must escape to infinity. This fact is true because of some elementary inequalities:
by the Triangle Inequality. Therefore
This last fact is true since |xn| - 1 > 1.
 2 Role of the Critical Orbit (Next Section)
2 Role of the Critical Orbit (Next Section) Fractal Geometry of the Mandelbrot Set (Cover Page)
Fractal Geometry of the Mandelbrot Set (Cover Page) Fractal Geometry of the Mandelbrot Set (Previous Section)
Fractal Geometry of the Mandelbrot Set (Previous Section)